广西柳州市柳江区2022年九年级数学一模考试试卷
试卷更新日期:2022-07-21 类型:中考模拟
一、单选题
-
1. 5的相反数是( )A、 B、 C、 D、52. 如图是由4个小正方体组合成的几何体,该几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、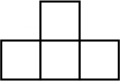 D、
D、 3. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
3. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 疫情未结束,防控别大意.自2020年新冠肺炎疫情发生以来,截止2022年3月18日,我国累计确诊病例420648例,累计死亡10625例,用科学记数法将数据10625表示为( )A、 B、 C、 D、5. 小明妈妈经营一家皮鞋专卖店,为了提高效益,小明帮妈妈对上个月各种型号的皮鞋销售数量进行了一次统计分析,决定在这个月的进货中多进某种型号皮鞋,此时小明应重点参考( )A、众数 B、平均数 C、加权平均数 D、中位数6. 的计算结果是( )A、 B、 C、 D、7. 不等式组的解集在数轴上表示为( )A、
4. 疫情未结束,防控别大意.自2020年新冠肺炎疫情发生以来,截止2022年3月18日,我国累计确诊病例420648例,累计死亡10625例,用科学记数法将数据10625表示为( )A、 B、 C、 D、5. 小明妈妈经营一家皮鞋专卖店,为了提高效益,小明帮妈妈对上个月各种型号的皮鞋销售数量进行了一次统计分析,决定在这个月的进货中多进某种型号皮鞋,此时小明应重点参考( )A、众数 B、平均数 C、加权平均数 D、中位数6. 的计算结果是( )A、 B、 C、 D、7. 不等式组的解集在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 8. 分式方程的解是( )A、 B、3 C、1 D、29. 一次函数的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
8. 分式方程的解是( )A、 B、3 C、1 D、29. 一次函数的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )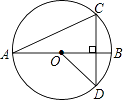 A、160° B、150° C、140° D、120°11. 通过如下尺规作图,能使的是( )A、
A、160° B、150° C、140° D、120°11. 通过如下尺规作图,能使的是( )A、 B、
B、 C、
C、 D、
D、 12. 如图,在正方形中,E,F分别是 , 的中点, , 交于点G,连接.下列结论:①;②;③.其中正确的结论是( )
12. 如图,在正方形中,E,F分别是 , 的中点, , 交于点G,连接.下列结论:①;②;③.其中正确的结论是( ) A、①② B、①③ C、②③ D、①②③
A、①② B、①③ C、②③ D、①②③二、填空题
-
13. 如图,直线a、b被第三条直线c所截,如果 , , 那么的度数是.
 14. 若式子 无意义,则x的取值范围是.15. 因式分解: .16. 一元二次方程的解是.17. 下表在我国宋朝数学家杨辉1261年的著作《解:九章算法》中提到过,因而人们把这个表叫做杨辉三角,请你根据杨辉三角的规律补全下表第四行空缺的数字是.
14. 若式子 无意义,则x的取值范围是.15. 因式分解: .16. 一元二次方程的解是.17. 下表在我国宋朝数学家杨辉1261年的著作《解:九章算法》中提到过,因而人们把这个表叫做杨辉三角,请你根据杨辉三角的规律补全下表第四行空缺的数字是.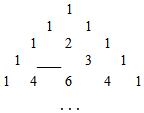 18. 如图,在平面直角坐标系中,A(﹣4,0),B(0,3),以点B为圆心、2为半径的⊙B有一动点P.连接AP,若点C为AP的中点,连接OC,则OC的最小值为 .
18. 如图,在平面直角坐标系中,A(﹣4,0),B(0,3),以点B为圆心、2为半径的⊙B有一动点P.连接AP,若点C为AP的中点,连接OC,则OC的最小值为 .
三、解答题
-
19. 计算:.20. 一次课外实践活动中,一个小组利用热气球的探测器测量一栋楼房的高度如图所示,热气球的探测器显示,从热气球看这栋楼楼顶的仰角为 , 看这栋楼底部的俯角为 , 热气球与楼的水平距离为100米,求这栋楼的高度(结果保留整数,参考数据: , ).
 21. 某中学食堂开设了两个窗口,窗口一提供四种食品:肉包、馒头、鸡蛋、油饼;窗口二提供两种食品:牛奶、豆浆. 约定:学生在一个窗口领一种食品后,再到另一个窗口领一种食品.(1)、问:学生早餐领到的食品一共有几种不同的可能?(2)、如果某天食堂师傅在两个窗口随机发放食品,请用列表或画树状图的方法,求出小王同学该天早餐刚好得到牛奶和馒头的概率.22. 为了解某校九年级男生的体能情况,体育老师从中随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成尚不完整的扇形图和条形图,根据图形信息回答下列问题:
21. 某中学食堂开设了两个窗口,窗口一提供四种食品:肉包、馒头、鸡蛋、油饼;窗口二提供两种食品:牛奶、豆浆. 约定:学生在一个窗口领一种食品后,再到另一个窗口领一种食品.(1)、问:学生早餐领到的食品一共有几种不同的可能?(2)、如果某天食堂师傅在两个窗口随机发放食品,请用列表或画树状图的方法,求出小王同学该天早餐刚好得到牛奶和馒头的概率.22. 为了解某校九年级男生的体能情况,体育老师从中随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成尚不完整的扇形图和条形图,根据图形信息回答下列问题: (1)、本次抽测的男生有人,抽测成绩的众数是;(2)、请将条形图补充完整;(3)、若规定引体向上6次以上(含6次)为体能达标,则该校125名九年级男生中估计有多少人体能达标?23. 如图,为了估算河岸相对的两点A,B的宽度,可以在河岸边取的垂线上的两点C,D,使 , 再画出的垂线 , 使E与A,C在一条直线上,这时测得米,求河宽.
(1)、本次抽测的男生有人,抽测成绩的众数是;(2)、请将条形图补充完整;(3)、若规定引体向上6次以上(含6次)为体能达标,则该校125名九年级男生中估计有多少人体能达标?23. 如图,为了估算河岸相对的两点A,B的宽度,可以在河岸边取的垂线上的两点C,D,使 , 再画出的垂线 , 使E与A,C在一条直线上,这时测得米,求河宽.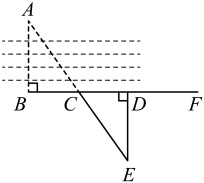 24. 如图,一次函数y1=ax+b与反比例函数y2=的图象交于A、B两点.点A的横坐标为2,点B的纵坐标为1.
24. 如图,一次函数y1=ax+b与反比例函数y2=的图象交于A、B两点.点A的横坐标为2,点B的纵坐标为1. (1)、求a,b的值.(2)、在反比例y2=第三象限的图象上找一点P,使点P到直线AB的距离最短,求点P的坐标.
(1)、求a,b的值.(2)、在反比例y2=第三象限的图象上找一点P,使点P到直线AB的距离最短,求点P的坐标.

