四川省南充市2021年中考数学诊断试卷

试卷更新日期：2022-07-21 类型：中考模拟

进入出卷网下载

一、单选题

1. 若﹣3a＝1，则a的值是（）

A、﹣ $\frac{1}{3}$ B、 $\frac{1}{3}$ C、3 D、﹣3

查看试题解析
2. 为纾解中小微企业困难，助力企业健康发展，高坪区严格实施减收失业保险费、积极发放稳岗补贴等政策，对不裁员、少裁员的企业，返还失业保险费，其中中小微企业返还率100%.截至3月29日，全区715户企业阶段性降费，惠及职工10400人.将10400用科学记数法表示为（）

A、1.04×10³ B、1.04×10⁴ C、10.5×10⁴ D、0.104×10⁵

查看试题解析
3. 一个几何体的三视图如图所示，则这个几何体是（）

A、四棱锥 B、四棱柱 C、三棱锥 D、三棱柱

查看试题解析
4. 下列运算正确的是（）

A、a²＋a³＝a⁵ B、（﹣a³）²＝a⁶ C、﹣2a⁶÷a²＝﹣2a³ D、（a＋b）²＝a²＋b²

查看试题解析
5. 下列说法正确的是（）

A、一个游戏中奖的概率是 $\frac{1}{100}$ ，则做100次这样的游戏一定会中奖 B、为了了解全国中学生的心理健康状况，应采用普查的方式 C、一组数据0，1，2，1，1的众数和中位数都是1 D、若甲组数据的方差S²＝0.2，乙组数据的方差S²＝0.5，则乙组数据比甲组数据稳定

查看试题解析
6. 如图，在△ABC中，∠BAC=90°，AD是高，BE是中线，CF是角平分线，CF交AD于点G，交BE于点H，下面说法不正确的是（）

A、△ABE的面积=△BCE的面积 B、∠AFG=∠AGF C、BH=CH D、∠FAG=2∠ACF

查看试题解析
7. 如图，在菱形ABCD中，∠B＝45°，AE⊥BC于点E，延长BC至B′，使EB′＝BE.连接AB′交CD交于点F.AB＝a.则B′F的长度为（）

A、 $\frac{2 a}{3}$ B、 $\frac{\sqrt{2}}{3} a$ C、（ $\sqrt{2} - 1$ ）a D、 $\frac{(2 - \sqrt{2})}{2} a$

查看试题解析
8. 已知关于x的不等式组 ${\begin{cases} x > 2 a - 3 \\ 2 x \geq 3 (x - 2) + 5 \end{cases}$ 仅有三个整数解，则a的取值范围是（）

A、 $\frac{1}{2}$ ≤a＜1 B、 $\frac{1}{2}$ ≤a≤1 C、 $\frac{1}{2}$ ＜a≤1 D、a＜1

查看试题解析
9. 如图，在Rt△ABC中，∠BAC=90°，AB=AC=3，将一个无限大的直角尺MON的直角顶点O与BC边上的中点D重合并绕点D旋转，分别交AB、AC所在的直线于E、F，连接EF，若BE＝1，则EF的长度为（）

A、 $\sqrt{5}$ B、 $\sqrt{17}$ C、 $\sqrt{17}$ 或 $\sqrt{5}$ D、无法确定

查看试题解析
10. 如图，二次函数y=ax²+bx+c的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，2）与（0，3）之间（不包括这两点），对称轴为直线x=2．下列结论：abc＜0；②9a+3b+c＞0；③若点M（ $\frac{1}{2}$ ，y₁），点N（ $\frac{5}{2}$ ，y₂）是函数图象上的两点，则y₁＜y₂；④﹣ $\frac{3}{5}$ ＜a＜﹣ $\frac{2}{5}$ ．其中正确结论有（）

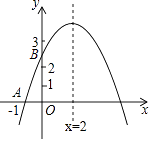A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 计算（1﹣ $\frac{b}{a}$ ）÷（a﹣b）＝.

查看试题解析
12. 有大小、形状、颜色完全相同的5个乒乓球，每个球上分别标有数字1、2、3、4、5中的一个，将这5个球放入不透明的袋中搅匀，如果不放回的从中随机连续抽取两个，则这两个球上的数字之和为偶数的概率是.

查看试题解析
13. 如图，数学活动课上，小明用边长为20cm的正五边形纸片材料制作圆锥，他以D为圆心，DC为半径作扇形DEC，将该扇形围成圆锥的侧面，则这个圆锥底面圆的半径是cm.

查看试题解析
14. 已知实数a²﹣3a﹣1＝0，则代数式a²﹣a﹣ $\frac{2}{a}$ 的值为.

查看试题解析
15. 抛物线y＝x²＋mx＋（m﹣1）与x轴交于点A（x₁ ， 0），B（x₂ ， 0），x₁＜x₂ ，与y轴交于点C，且满足x₁²＋x₂²＋x₁x₂＝7，则△ABC的面积为.

查看试题解析
16. 如图，边长为4的正方形ABCD中，点E在BC边上，CE＝1，将△DCE沿DE折叠得△DFE，再将△DCE按顺时针方向绕点D旋转90度，连接EG、FG，则下列说法：①∠GEF＝∠AGE；②GF＝5；③tan∠FGB＝ $\frac{36}{77}$ ；④∠FGB＝∠ADG；其中正确结论为（填序号）.

查看试题解析

三、解答题

17. 计算： ${(\frac{1}{2})}^{- 1} - | 1 - \sqrt{3} |$ ＋6tan30°﹣ $(3 - \sqrt{27})^{0}$ .

查看试题解析
18. 如图，点E，F在BC上，BE＝CF，AB＝DC，∠B＝∠C，求证：AF＝DE.

查看试题解析
19. 随着扶贫工作的深入，全国近800万脱贫家庭子女接受了职业教育培训.通过“授人以渔”的职业技能教育“智”拔穷根，实现了一人稳定就业，全家基本脱贫的扶贫目标.某市以就业为导向，量身定做培训“菜单”，采取多种方式，实现培训就业一体化，着力提高培训的针对性和实效性，拟制了下列四种方式：A：劳动技能培训班；B：岗位＋劳务机构＋培训；C：互联网＋职业技能培训；D：帮带培训.该市某职业技术培训中心对前来报名参加2021年第一期培训的学员选择的培训方式绘制成了两幅不完整的统计图，根据图中信息解答下列各题：

(1)、参加该职业技术培训中心2021年第一期培训的学员共有多少人？

(2)、请你将条形统计图2补充完整；

(3)、培训结束时，该培训中心决定在方式B中选出优秀男学员2名，在方式C中选出优秀女学员2名，现从这4名优秀学员中选择2名作劳动技能展示，请用列举法（画树状图或列表）求出抽到的两名学员都是男学员的概率.

查看试题解析
20. 已知x₁ ， x₂是一元二次方程4kx²﹣4kx＋k＋2＝0的两个实数根.

(1)、求k的取值范围；

(2)、求使 $\frac{x_{1}}{x_{2}} + \frac{x_{2}}{x_{1}} - 2$ 的值为整数的实数k的最大整数值.

查看试题解析
21. 如图，一次函数y=x+4的图象与反比例函数y= $\frac{k}{x}$ （k为常数且k≠0）的图象交于A（﹣1，a），B两点，与x轴交于点C．

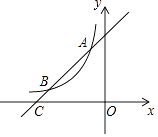(1)、求此反比例函数的表达式；

(2)、若点P在x轴上，且S_△ACP= $\frac{3}{2}$ S_△BOC ，求点P的坐标．

查看试题解析
22. 如图，在△ABC中，O为AC上一点，以点O为圆心，OC为半径作圆，与BC相切于点C，过点A作AD⊥BO交BO的延长线于点D，且∠AOD=∠BAD.

(1)、求证：AB为⊙O的切线；

(2)、若BC=6，tan∠ABC= $\frac{4}{3}$ ，求AD的长.

查看试题解析
23. 2020年一场突如其来的新冠病毒在全球蔓延，我国政府以人为本，领导全国人民打了一场卓越的抗疫阻击战，取得了阶段性的成果.在疫情期间，某市政府对销售防疫产品的商店进行补贴，该市规定销售某一消毒液销售价不高于45元/件可获政府补贴金5元/件，已知这种产品的成本价为30元/件.每天销售量y（件）与销售单价x（元/件）之间存在一次函数关系，如图所示.

(1)、求这种产品每天的销售量y（单位：件）与销售单价x（单位：元/件）之间的函数关系.

(2)、这种产品销售单价定为多少元时，商店每天的销售利润既最大，又能获得政府补贴？商店共获利多少元？

查看试题解析
24. 如图，在矩形ABCD中，点E为AB上一点，过点D作DP⊥CE于点P，连接DE交AP于点F，若点P恰好为CE的中点时.

(1)、求证：△ABP是直角三角形；

(2)、若BC＝3，BE＝1，求 $\frac{S_{△ A E F}}{S_{△ A F D}}$ 的值；

(3)、如图②，在（2）的条件下，如果点G、Q分别为DP、DE上的动点，求GF+GQ的最小值.

查看试题解析
25. 如图，在平面直角坐标系中，抛物线y＝﹣x²＋bx＋c经过点A（4，0）、B（0，4）、C.其对称轴l交x轴于点D，交直线AB于点F，交抛物线于点E.

(1)、求抛物线的解析式；

(2)、点P为直线l上的动点，求△PBC周长的最小值；

(3)、点N为直线AB上的一点（点N不与点F重合），在抛物线上是否存在一点M，使以点E、F、N、M为顶点的四边形为平行四边形？若存在，直接写出点M的坐标，若不存在，说明理由.

查看试题解析