(人教版)2022-2023学年度第一学期九年级数学23.2.2 中心对称图形 同步测试
试卷更新日期:2022-07-21 类型:单元试卷
一、单选题
-
1. 垃圾分类是资源,垃圾混置是垃圾.下列可回收物、有害垃圾、厨余垃圾、其他垃圾四种垃圾回收标识中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
2. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、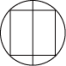 B、
B、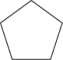 C、
C、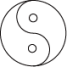 D、
D、 3. 下面四个图形中,既是轴对称图形也是中心对称图形的是( )A、
3. 下面四个图形中,既是轴对称图形也是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列各曲线是在平面直角坐标系xOy中根据不同的方程绘制而成的,其中是中心对称图形的是( )A、
4. 下列各曲线是在平面直角坐标系xOy中根据不同的方程绘制而成的,其中是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列图形中,既是中心对称图形也是轴对称图形的是( )A、圆 B、平行四边形 C、直角三角形 D、等边三角形6. 下列图形中,不是中心对称图形的是( )A、
5. 下列图形中,既是中心对称图形也是轴对称图形的是( )A、圆 B、平行四边形 C、直角三角形 D、等边三角形6. 下列图形中,不是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 下列说法正确的是( )A、全等的两个图形成中心对称 B、旋转后能够重合的两个图形成中心对称 C、成中心对称的两个图形旋转后必重合 D、旋转后的图形对应线段平行8. 如图, 与 关于O成中心对称,下列结论中不一定成立的是( )
7. 下列说法正确的是( )A、全等的两个图形成中心对称 B、旋转后能够重合的两个图形成中心对称 C、成中心对称的两个图形旋转后必重合 D、旋转后的图形对应线段平行8. 如图, 与 关于O成中心对称,下列结论中不一定成立的是( ) A、 B、 C、 D、9. 2021年国庆节期间,许多单位用鲜花围成了几何图形庆祝祖国母亲72周岁生日下列围成的几何图形中既是轴对称图形,又是中心对称图形的是( )A、等腰三角形 B、平行四边形 C、矩形 D、正五边形10. 下列图形:①平行四边形、②矩形、③正方形、④等边三角形,其中,既是轴对称图形又是中心对称图形的有( )A、①② B、②③ C、③④ D、①④
A、 B、 C、 D、9. 2021年国庆节期间,许多单位用鲜花围成了几何图形庆祝祖国母亲72周岁生日下列围成的几何图形中既是轴对称图形,又是中心对称图形的是( )A、等腰三角形 B、平行四边形 C、矩形 D、正五边形10. 下列图形:①平行四边形、②矩形、③正方形、④等边三角形,其中,既是轴对称图形又是中心对称图形的有( )A、①② B、②③ C、③④ D、①④二、填空题
-
11. 如图,正方形ABCD旋转后能与正方形CDEF重合,那么点A,B,C,D中,可以作为旋转中心的有个.
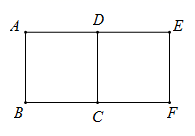 12. 如图,将n个边长都为1cm的正方形按如图所示摆放,点A1, A2,…,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为
12. 如图,将n个边长都为1cm的正方形按如图所示摆放,点A1, A2,…,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为 13. 点O是平行四边形ABCD的对称中心,AD>AB,E、F分别是AB边上的点,且EF= AB;G、H分别是BC边上的点,且GH= BC;若S1 , S2分别表示∆EOF和∆GOH的面积,则S1 , S2之间的等量关系是
13. 点O是平行四边形ABCD的对称中心,AD>AB,E、F分别是AB边上的点,且EF= AB;G、H分别是BC边上的点,且GH= BC;若S1 , S2分别表示∆EOF和∆GOH的面积,则S1 , S2之间的等量关系是 14. 如图, 与 关于点 成中心对称,若 ,则 .
14. 如图, 与 关于点 成中心对称,若 ,则 .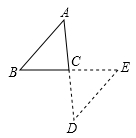 15. 若点P(﹣2,b)与点M(a,3)关于原点对称,则a+b= .
15. 若点P(﹣2,b)与点M(a,3)关于原点对称,则a+b= .三、解答题
-
16. 直角坐标系第二象限内的点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,试求x+2y的值.17.
已知点A的坐标为( ,0),把点A绕着坐标原点顺时针旋转135º到点B,求点B的坐标.
18. 如图所示,已知MN⊥PQ于点O,点A、 是以MN为轴的对称点,而点 、A是以PQ为轴的对称点,求证:点 、 是以点O为对称中心的对称点.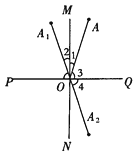 19.
19.如图,已知∠ABC和点P,求作:
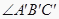 ,使
,使 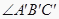 与∠ABC关于点P对称.
与∠ABC关于点P对称. 20.
20.如下图所示,在平行四边形ABCD中,AE⊥BC,CF⊥AD,M、N分别是AB、DC的中点.求证:MN与EF互相平分.
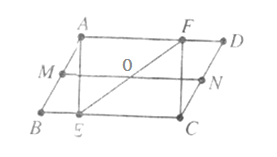
四、综合题
-
21. 如图,已知线段 , 点A在线段上,且 , 点B为线段上的一个动点.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,旋转角分别为和 . 若旋转后M、N两点重合成一点C(即构成),设 .
 (1)、的周长为;(2)、若 , 求x的值.22. 在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)、的周长为;(2)、若 , 求x的值.22. 在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)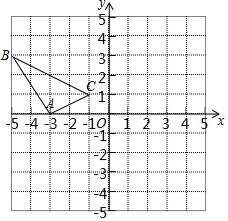 (1)、先作△ABC关于原点O成中心对称的△A1B1C1 , 再把△A1B1C1向上平移4个单位长度得到△A2B2C2;(2)、△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.
(1)、先作△ABC关于原点O成中心对称的△A1B1C1 , 再把△A1B1C1向上平移4个单位长度得到△A2B2C2;(2)、△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.

