（人教版）2022-2023学年度第一学期九年级数学23.2.1 中心对称 同步测试
试卷更新日期：2022-07-20 类型：同步测试
一、单选题
-
1. 下列图形中，是中心对称图形，但不是轴对称图形的是（ ）A、
B、
C、
D、
2. 在下列图形中，既是中心对称图形又是轴对称图形的是（ ）A、
B、
C、
D、
3. 数学世界奇妙无穷，其中曲线是微分几何的研究对象之一，下列数学曲线既是轴对称图形，又是中心对称图形的是（ ）A、
B、
C、
D、
4. 下列图形中，中心对称图形是（ ）A、
B、
C、
D、
5. 下列既是轴对称图形又是中心对称图形的是（ ）A、等腰三角形 B、等边三角形 C、平行四边形 D、正方形6. 下列图形中，既是轴对称图形，又是中心对称图形的是（ ）A、
B、
C、
D、
7. 下列图形中，既是轴对称图形，又是中心对称图形的是（ ）A、
B、
C、
D、
8. 如图，在下面的扑克牌中，牌面是中心对称图形的有（ ）
A、2张 B、3张 C、4张 D、5张9. “垃圾分类，利国利民”，在2019年7月1日起上海开始正式实施垃圾分类，到2020年底先行先试的46个重点城市，要基本建成垃圾分类处理系统．以下四类垃圾分类标志的图形，其中既是轴对称图形又是中心对称图形的是（ ）
A、可回收物 B、有害垃圾 C、厨余垃圾 D、其他垃圾10. 2022年冬奥会将在我国北京市和张家口市联合举行，下列历届冬奥会会徵的部分图案中，是中心对称图形的是（ ）A、
B、
C、
D、
二、填空题
-
11. 写出一个四边形，使它既是中心对称图形又是轴对称图形，则这个四边形可能是 ．12. 给出以下4个图形：①等边三角形，②平行四边形，③菱形，④正方形．其中既是轴对称图形又是中心对称图形的是 ． （填写序号）13. 如图，△ABC和△DEC关于点C成中心对称，若AC＝1，AB＝2，∠BAC＝90°，则AE的长是.
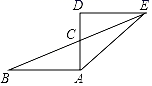14. 如图，所示的美丽图案中，既是轴对称图形又是中心对称图形的有个.
15. 如图，在平面直角坐标系中，抛物线y=x2+mx交x轴的负半轴于点A．点B是y轴正半轴上一点，点A关于点B的对称点A′恰好落在抛物线上．过点A′作x轴的平行线交抛物线于另一点C．若点A′的横坐标为1，则A′C的长为 ．
三、解答题
-
16. 如图
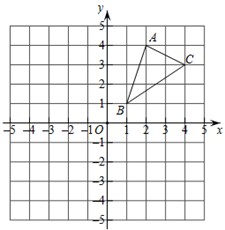
（1）请画出△ABC关于原点O对称的△A1B1C1；
（2）请画出△ABC绕点B逆时针旋转90°后的△A2BC2；
（3）写出A2 和C2两点坐标．17. 如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A（1，1），B（4，1），C（3，3）．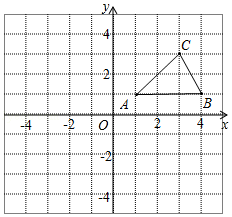
(1)、将△ABC向下平移5个单位后得到△A1B1C1 ， 请画出△A1B1C1；(2)、将△ABC绕原点O逆时针旋转90°后得到△A2B2C2 ， 请画出△A2B2C2；(3)、判断以O，A1 ， B为顶点的三角形的形状．（无须说明理由）18. 在4×4的方格纸中，△ABC的三个顶点都在格点上．
(1)、在图1中画出与△ABC成轴对称且与△ABC有公共边的格点三角形（画出一个即可）；(2)、将图2中的△ABC绕着点C按顺时针方向旋转90°，画出经旋转后的三角形．19.如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（3，﹣1）．以原点O为对称中心，画出△ABC关于原点O对称的△A′B′C′，并写出A′、B′、C′的坐标．
20. 如图所示，方格纸中的每个小方格都是边长为1个单位长度的正方形，建立平面直角坐标系，△ABC的顶点均在格点上．（不写作法）①以原点O为对称中心，画出△ABC关于原点O对称的△A1B1C1 ， 并写出B1的坐标；
②再把△A1B1C1绕点C1 ， 顺时针旋转90°，得到△A2B2C2 ， 请你画出△A2B2C2 ， 并写出B2的坐标．
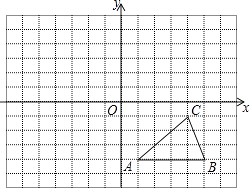21. 如图，已知△ABC的顶点A，B，C的坐标分别是A（﹣1，﹣1），B（﹣4，﹣3），C（﹣4，﹣1）．
（1）作出△ABC关于原点O中心对称的图形；
（2）将△ABC绕原点O按顺时针方向旋转90°后得到△A1B1C1 ， 画出△A1B1C1 ， 并写出点A1的坐标．22. 如图，在平面直角坐标系中，已知 ABC的三个顶点的坐标分别为A（－1，1），B（－3，1），C（－1，4）．
①画出△ABC关于y轴对称的△A1B1C1；
②将△ABC绕着点B顺时针旋转90°后得到△A2BC2 ， 请在图中画出△A2BC2 ， 并求出线段BC旋转过程中所扫过的面积（结果保留 ）
