（人教版）2022-2023学年度第一学期九年级数学23.1 图形的旋转同步测试

试卷更新日期：2022-07-20 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，在 $△ A B C$ 中， $∠ B A C = 75^{\circ}$ ，以点 $A$ 为旋转中心，将 $△ A B C$ 绕点 $A$ 逆时针旋转得到 $△ A D E$ ，点 $B 、 C$ 的对应点分别为 $D 、 E$ ，连接 $C E$ ，若 $C E / / A B$ ，则 $∠ C A E$ 的值是（）

A、 $25^{\circ}$ B、 $30^{\circ}$ C、 $35^{\circ}$ D、 $45^{\circ}$

查看试题解析
2. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 30 °$ ，将 $△ A B C$ 绕点C逆时针旋转90°得到 $△ D E C$ ，则 $∠ A E D$ 的度数为（）

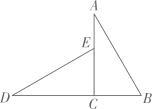A、105° B、120° C、135° D、150°

查看试题解析
3. 如图，在Rt△ABC中，∠BAC＝90°，将△ABC绕点A顺时针旋转90°后得到的△AB′C′（点B的对应点是点B′，点C的对应点是点C′），连接CC′．若∠CC′B′＝20°，则∠B的大小是（）

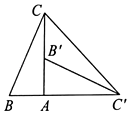A、70° B、65° C、60° D、55°

查看试题解析
4. 如图，将△ABC绕点A按逆时针方向旋转得到 $△ A B C$ ．若点 $B$ 刚好落在BC边上，且 $A B = C B^{'}$ ，若∠C=20°，则△ABC旋转的角度为（）

A、60° B、80° C、100° D、120°

查看试题解析
5. 如图，将△AOB绕点O按逆时针方向旋转60°后得到 $△ A O B$ ，若∠AOB＝25°，则 $∠ A O B^{^{'}}$ 的度数是（）

A、25° B、35° C、40° D、85°

查看试题解析
6. 如图，在正方形网格中，格点 $△ A B C$ 绕某点顺时针旋转 $α$ 度 $(0 < α < 18 0^{°})$ ，得到格点 $Δ A_{1} B_{1} C_{1}$ ，点 $A$ 与点 $A_{1}$ ，点 $B$ 与点 $B_{1}$ ，点 $C$ 与点 $C_{1}$ 是对应点，则 $α$ 的值为( ）

A、 $5 0^{°}$ B、 $6 0^{°}$ C、 $9 0^{°}$ D、 $12 0^{°}$

查看试题解析
7. 如图，将矩形ABCD绕点B按顺时针方向旋转一定角度得到矩形 $A B C D$ ．此时点A的对应点 $A$ 恰好落在对角线AC的中点处．若AB＝3，则点B与点 $D$ 之间的距离为（）

A、3 B、6 C、 $3 \sqrt{3}$ D、 $6 \sqrt{3}$

查看试题解析
8. 下列运动中，属于旋转运动的是（）

A、小明向北走了 4 米 B、一物体从高空坠下 C、电梯从 1 楼到 12 楼 D、小明在荡秋千

查看试题解析
9. 如图，在Rt△ABC中，∠C＝90°，∠ABC=30°，AC＝ $\sqrt{3}$ ，将Rt△ABC绕点A逆时针旋转得到Rt△AB'C'，连接BB'，则BB'的长度是（）

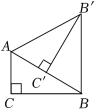A、1 B、3 C、 $\sqrt{3}$ D、2 $\sqrt{3}$

查看试题解析
10. 如图， $△$ ABC中，∠ACB＝90°，∠ABC＝40°．将 $△$ ABC绕点B逆时针旋转得到 $△ A^{'} B C^{'}$ ，使点C的对应点 $C^{'}$ 恰好落在边AB上，则 $∠ B A^{'} A$ 的度数是（）

A、50° B、70° C、110° D、120°

查看试题解析

二、填空题

11. 如图，在平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上， $∠ A O B = ∠ B = 30 ° ， O B = 4$ ．将 $△ A O B$ 绕点O逆时针旋转 $90 °$ ，点B的对应点 $B$ 的坐标是．

查看试题解析
12. 如图，将△ABC绕点C逆时针旋转得到△A′B′C，其中点A′与A是对应点，点B′与B是对应点，点A′落在直线BC上，连接AB′，若∠ACB＝45°，AC＝3，BC＝2，则AB′的长为．

查看试题解析
13. 如图， $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A B C = 40 °$ ．将 $△ A B C$ 绕点B逆时针旋转得到 $△ A' B C'$ ，使点C的对应点 $C'$ 恰好落在边AB上，则 $∠ B A' A$ 的度数是．

查看试题解析
14. 如图，将矩形 $A B C D$ 绕点A顺时针旋转到矩形 $A B^{^{'}} C^{^{'}} D^{^{'}}$ 的位置，旋转角为 $α (0 ° < α < 90 °)$ ．若 $∠ 1 = 110 °$ ，则 $α$ 的大小为（度）．

查看试题解析
15. 如图所示， $△ A B C$ 绕点P顺时针旋转得到 $△ D E F$ ，则旋转的角度是．

查看试题解析

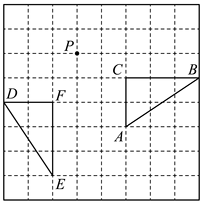
三、解答题

16. 在△ABC中，AB＝BC＝4，∠ABC＝90°，M是AC的中点，点N在边AB上（不与点A，B重合），将△ANM绕点M逆时针旋转90°得到△BPM．
问：△BPN的面积能否等于3，请说明理由．

查看试题解析
17. 如图，在△ABC中，∠ABC＝90°，将△ABC绕点C顺时针旋转得到△DEC，连接AD，BE，延长BE交AD于点F．求证：∠DEF＝∠ABF．

查看试题解析
18. 如图将 $△ A B C$ 绕点A逆时针旋转得到 $△ A D E$ ，点C和点E是对应点，若 $∠ C A E = 90 °$ ， $A B = 1$ ，求BD的长．

查看试题解析
19. 如图，在Rt $△$ ABC中，∠ACB＝90°， $△$ EDC是 $△$ ABC绕着点C顺时针方向旋转90°得到的，若AB＝5，AC＝4，求BE的长．

查看试题解析
20. $△ A C B$ 中， $∠ C = 90 °$ ，以点A为中心，分别将线段 $A B$ ， $A C$ 逆时针旋转 $60 °$ 得到线段 $A D$ ， $A E$ ，连接 $D E$ ，延长 $D E$ 交 $C B$ 于点 $F$ ．用等式表示线段 $C F$ 与 $A C$ 的数量关系，并加以证明．

查看试题解析
21. 如图，四边形ABCD是正方形， $Δ$ ABE是等边三角形，M为对角线BD（不含B、D点）上任意一点，将线段BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM．
求证：AM=EN．

查看试题解析
22. 如图，O是四边形ABCD内一点，E是CD边的中点，分别连接OA，OB，OC，OD，OE，已知OA=OD，OB=OC，∠AOB+∠COD=180°．求证：OE= $\frac{1}{2}$ AB．

查看试题解析
23. 如图所示，将Rt△ABC绕点A顺时针旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上.若AC $= \sqrt{3}$ ，∠B＝60°，求CD的长.

查看试题解析
24. 如图，在等边 $Δ A B C$ 中， $D$ 是边 $A C$ 上的一点，连接 $B D$ ，将 $Δ B C D$ 绕点 $B$ 逆时针旋转60°得到 $Δ B A E$ ，连接 $E D$ ．若 $B C = 7 ， B D = 6$ ，求 $Δ A E D$ 的周长．

查看试题解析

（人教版）2022-2023学年度第一学期九年级数学23.1 图形的旋转 同步测试

一、单选题

二、填空题

三、解答题

（人教版）2022-2023学年度第一学期九年级数学23.1 图形的旋转同步测试