浙江省杭州市临平区2021-2022学年七年级下学期数学5月月考试卷

试卷更新日期：2022-07-20 类型：月考试卷

进入出卷网下载

一、选择题：本大题有10个小题，每小题3分，共30分．

1. 某种芯片每个探针单元的面积为0.00 000 64cm² ， 0.00 000 64用科学记数法表示为（）

A、6.4×10^－5 B、6.4×10⁶ C、6.4×10^－6 D、6.4×10⁵

查看试题解析
2. 若 $\{\begin{cases} x = 1 \\ y = 2 \end{cases}$ 是关于x，y的方程2x－y＋2a＝0的一个解，则常数a为（）

A、0 B、1 C、2 D、3

查看试题解析
3. 如图，下列判断错误的是（）

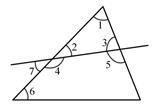A、∠1和∠2是同旁内角 B、∠3和∠4是内错角 C、∠5和∠6是同旁内角 D、∠5和∠7是同位角

查看试题解析
4. 若x²－ax－5＝(x－5)(x＋1)，则a为（）

A、4 B、－4 C、6 D、－6

查看试题解析
5. 如图，如果∠B＝∠AEF，下面结论正确的是（）

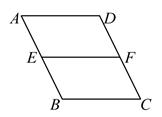A、AD∥BC B、AD∥EF C、BC∥EF D、AB∥CD

查看试题解析
6. 若x²＋2(2p－3)x＋4是完全平方式，则p的值等于（）

A、 $\frac{5}{2}$ B、2 C、2或1 D、 $\frac{5}{2}$ 或 $\frac{1}{2}$

查看试题解析
7. 下列从左到右变形正确的是（）

A、 $\frac{3 b}{a}$ ＝ $\frac{3 b c}{a c}$ B、 $\frac{3 a b}{a^{2}}$ ＝ $\frac{3 b}{a}$ C、 $\frac{3 b}{a}$ ＝ $\frac{3 b + c}{a + c}$ D、 $\frac{3 b}{a}$ ＝ $\frac{3 b^{2}}{a^{2}}$

查看试题解析
8. 若(3x＋2)(3x＋a)的化简结果中不含x的一次项，则常数a的值为（）

A、－2 B、－1 C、0 D、2

查看试题解析
9. 如图，已知直线AB，CD被直线AC所截，AB∥CD，E是平面内任意一点 (点E不在直线AB，CD，AC上)，设∠BAE＝α，∠DCE＝β．下列各式：
①α＋β，②α－β，③β－α，④360°－α－β，

则∠AEC的度数可能是（）

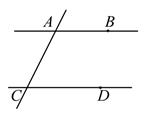A、①②③ B、①②④ C、①③④ D、①②③④

查看试题解析
10. 已知关于x，y的方程组 $\{\begin{cases} x + y = 1 + 4 a \\ 2 x - y = - a - 7 \end{cases}$ ，有下列结论：
①当a＝0时方程组的解是方程x＋y＝1的解；②当x＝y时，a＝ $- \frac{5}{2}$ ；③当x^y＝1，则a的值为3或－3；④不论a取什么实数3x－y的值始终不变．其中正确的是（）

A、①②③ B、①②④ C、②③④ D、①③④

查看试题解析

二、填空题：本大题有6个小题，每小题4分，共24分．

11. 3x²y•（）＝18x⁴y³ ．

查看试题解析
12. 已知a+b＝8，ab＝15，则a²+b²＝．

查看试题解析
13. 如图，直线l₁∥l₂ ， ∠1＝20°，则∠2＋∠3＝．

查看试题解析
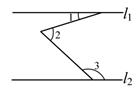14. 已知 $\frac{1}{a} + \frac{1}{b} = \frac{1}{c}$ ，则b＝． (用含有a，c的代数式表示)

查看试题解析
15. 如图，将长方形ABCD折叠，折痕为EF，BC的对应边B'C'与CD交于点M，若∠DMB'＝50°，则∠BEF的度数是．

查看试题解析
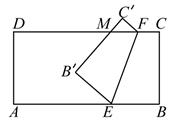16. 如图，在面积为56的长方形ABCD中放入边长分别为6和4的正方形AEFG和CMNK，若三块阴影部分的面积之和为16，则长方形的周长为．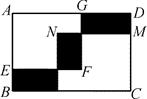

查看试题解析

三、解答题：本题有7小题，共66分．解答应写出文字说明、证明过程或演算步骤．

17. 计算：

(1)、 ${(- 0.5)}^{2} \div {(- \frac{1}{2})}^{- 3}$

(2)、 $\frac{3}{x^{2} - 4 x + 4} \div \frac{2 x + 4}{x^{2} - 4}$

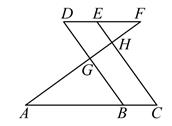
查看试题解析
18. 解下列方程(组)：

(1)、 $\{\begin{cases} 3 x - y = 17 \\ 2 x + 3 y = 4 \end{cases}$

(2)、 $\frac{1}{x - 3} + 2 = \frac{x - 4}{x - 3}$

查看试题解析
19. 因式分解：

(1)、4m²n³＋2m³n³

(2)、2a²(b－2)－8b＋16．

查看试题解析
20.

(1)、化简求值：(x＋2y)(x－2y)－(－x－3y)² ，其中x＝ $\frac{1}{3}$ ，y＝1．

(2)、已知2x－y＝1，xy＝2，求4x³ y－4x²y²＋xy³的值．

查看试题解析
21. 如图，点B，E分别在AC，DF上，BD，CE分别交AF于点G，H，∠AGB＝∠EHF，∠C＝∠D．求证：AC∥DF．

查看试题解析
22. 某广场计划在广场内种植A，B两种花木共6600棵，若A花木数量是B花木数量的2倍少600棵．

(1)、A，B两种花木的数量分别是多少棵？

(2)、如果安排26人同时种植这两种花木，每人每天能种植A花木60棵或B花木40棵，应分别安排多少人种植A花木和B花木，才能确保同时完成各自的任务？

查看试题解析
23. 已知直线AB与直线CD平行．

(1)、如图1，E为AB，CD之间一点，连接BE，DE，得到∠BED．
求证：∠BED＝∠B＋∠D；

(2)、如图，连接AD，BC，BF平分∠ABC，DF平分∠ADC，直线BF，DF交于点F．
①如图2，点B在点A的左侧，若∠ABC＝50°，∠ADC＝60°，求∠BFD的度数．

②如图3，点B在点A的右侧，设∠ABC＝α，∠ADC＝β，求∠BFD的度数．(用含有α，β的式子表示)

查看试题解析