山东省淄博市张店区2020-2021学年七年级上学期期末数学试题
试卷更新日期:2022-07-20 类型:期末考试
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 下列各数中,最小的数是( )A、 B、 C、 D、3. 用一个平面去截一个几何体,截面不可能是圆的几何体的是( )A、
 B、
B、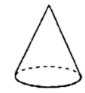 C、
C、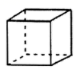 D、
D、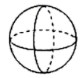 4. 某地区一天三次测量气温如下,早上是 , 中午上升了 , 半夜下降了 , 则半夜的气温是( )A、 B、 C、 D、5. 如图,数轴上的单位长度为1,有三个点A、B、C,若点A、C表示的数互为相反数,则图中点B对应的数是( )
4. 某地区一天三次测量气温如下,早上是 , 中午上升了 , 半夜下降了 , 则半夜的气温是( )A、 B、 C、 D、5. 如图,数轴上的单位长度为1,有三个点A、B、C,若点A、C表示的数互为相反数,则图中点B对应的数是( ) A、-1 B、0 C、1 D、36. 下面四个整式中,不能表示图中(图中图形均为长方形)阴影部分面积的是( )
A、-1 B、0 C、1 D、36. 下面四个整式中,不能表示图中(图中图形均为长方形)阴影部分面积的是( ) A、 B、 C、 D、7. 下列变形正确的是( )A、 B、 C、 D、8. 如图,“ 、 、 ”分别表示三种不同的物体 已知前两架天平保持平衡,要使第三架也保持平衡 如果在“?”处只放“ ”,那么应放“ ”
A、 B、 C、 D、7. 下列变形正确的是( )A、 B、 C、 D、8. 如图,“ 、 、 ”分别表示三种不同的物体 已知前两架天平保持平衡,要使第三架也保持平衡 如果在“?”处只放“ ”,那么应放“ ” A、3个 B、4个 C、5个 D、6个9. 下列方程变形正确的是( )A、方程 未知数系数化为1,得 B、方程 去括号,得 C、方程 去分母,得 D、方程 可化成10. 下图给出的是2021年某月份的日历表,任意圈出一竖列上相邻的三个数,请你运用方程思想来研究,发现这三个数的和不可能是( )
A、3个 B、4个 C、5个 D、6个9. 下列方程变形正确的是( )A、方程 未知数系数化为1,得 B、方程 去括号,得 C、方程 去分母,得 D、方程 可化成10. 下图给出的是2021年某月份的日历表,任意圈出一竖列上相邻的三个数,请你运用方程思想来研究,发现这三个数的和不可能是( ) A、27 B、41 C、42 D、6911. 某商品的价格标签已丢失,售货员只知道它的进价为80元,打七折售出后,仍可获利5%,你认为标签上的价格为( )元.A、110 B、120 C、130 D、14012. 如图是一个运算程序的示意图,若开始输入的x值为81,我们看到第一次输出的结果为27,第二次输出的结果为9,…,第2021次输出的结果为( )
A、27 B、41 C、42 D、6911. 某商品的价格标签已丢失,售货员只知道它的进价为80元,打七折售出后,仍可获利5%,你认为标签上的价格为( )元.A、110 B、120 C、130 D、14012. 如图是一个运算程序的示意图,若开始输入的x值为81,我们看到第一次输出的结果为27,第二次输出的结果为9,…,第2021次输出的结果为( ) A、1 B、3 C、9 D、27
A、1 B、3 C、9 D、27二、填空题
-
13. 单项式的系数是 , 次数是 .14. 若与是同类项,则m的值是 .15. 若是关于x的方程的解,则 .16. 把这9个数填入方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”,它源于我国古代的“洛书”(图1),是世界上最早的“幻方”.图2是仅可以看到部分数值的“九宫格”,则x= .
 17. 下列图形都是由同样大小的黑色正方形纸片组成,其中第1个图形中有3张黑色正方形纸片,第2个图形中有5张黑色正方形纸片,第3个图形中有7张黑色正方形纸片,…,按此规律排列下去,第n个图形中黑色正方形纸片的张数为 .
17. 下列图形都是由同样大小的黑色正方形纸片组成,其中第1个图形中有3张黑色正方形纸片,第2个图形中有5张黑色正方形纸片,第3个图形中有7张黑色正方形纸片,…,按此规律排列下去,第n个图形中黑色正方形纸片的张数为 .
三、解答题
-
18. 解答下列各题:(1)、计算:(2)、先化简,再求值: , 其中 , , .19. 解方程:(1)、4-3(2-x)=5x(2)、-=120. 用5个相同的正方体搭成如图所示的几何体.
 (1)、分别画出从正面、左面、上面看到的几何体的形状图.(2)、在这个几何体中,再添加一个相同的正方体组成一个新几何体,使从正面,左面看这个新几何体时,看到的形状图与原来相同,且从上面看到的形状图与原来不同.请画出从上面看到的这个新几何体的形状图.21. “地摊经济”刺激了经济的复苏.今年国庆周期间,小王用2000元购进了一批商品,在夜市摆地摊售卖8天,全部销售完毕.每天的收入以300元为标准,超过的钱数记作正数,不足的钱数记作负数,8天的收入记录如下:+62,+40,﹣60,﹣38,0,+34,+8,﹣54.(单位:元)(1)、收入最多的一天比最少的一天多多少钱?(2)、小王这8天的地摊收入是盈利还是亏损?盈利或亏损多少钱?22. 结合数轴与绝对值的知识回答下列问题:
(1)、分别画出从正面、左面、上面看到的几何体的形状图.(2)、在这个几何体中,再添加一个相同的正方体组成一个新几何体,使从正面,左面看这个新几何体时,看到的形状图与原来相同,且从上面看到的形状图与原来不同.请画出从上面看到的这个新几何体的形状图.21. “地摊经济”刺激了经济的复苏.今年国庆周期间,小王用2000元购进了一批商品,在夜市摆地摊售卖8天,全部销售完毕.每天的收入以300元为标准,超过的钱数记作正数,不足的钱数记作负数,8天的收入记录如下:+62,+40,﹣60,﹣38,0,+34,+8,﹣54.(单位:元)(1)、收入最多的一天比最少的一天多多少钱?(2)、小王这8天的地摊收入是盈利还是亏损?盈利或亏损多少钱?22. 结合数轴与绝对值的知识回答下列问题: (1)、数轴上表示4和1的两点之间的距离是;表示-3和2两点之间的距离是;一般地,数轴上表示数m和数n的两点之间的距离等于(2)、如果表示数a和-2的两点之间的距离是3,求a的值(3)、若数轴上表示数a的点位于-4与2之间,求的值.23. 阅读材料:我们知道, , 类似地,我们把看成一个整体,则 , “整体思想”是中学教学课题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.(1)、尝试应用:把看成一个整体,合并的结果是 .(2)、已知 , 求的值.(3)、拓展探索:已知 , , , 求的值.24. 为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现,甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球,乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.(1)、求每套队服和每个足球的价格是多少?(2)、若城区四校联合购买100套队服和个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;(3)、在(2)的条件下,若 , 假如你是本次购买任务的负责人,你认为到甲、乙哪家商场购买比较合算?
(1)、数轴上表示4和1的两点之间的距离是;表示-3和2两点之间的距离是;一般地,数轴上表示数m和数n的两点之间的距离等于(2)、如果表示数a和-2的两点之间的距离是3,求a的值(3)、若数轴上表示数a的点位于-4与2之间,求的值.23. 阅读材料:我们知道, , 类似地,我们把看成一个整体,则 , “整体思想”是中学教学课题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.(1)、尝试应用:把看成一个整体,合并的结果是 .(2)、已知 , 求的值.(3)、拓展探索:已知 , , , 求的值.24. 为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现,甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球,乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.(1)、求每套队服和每个足球的价格是多少?(2)、若城区四校联合购买100套队服和个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;(3)、在(2)的条件下,若 , 假如你是本次购买任务的负责人,你认为到甲、乙哪家商场购买比较合算?