山东省淄博市临淄区2020-2021学年七年级上学期期末数学试题
试卷更新日期:2022-07-20 类型:期末考试
一、单选题
-
1. 下列实数中,最小的是( )A、0 B、 C、 D、12. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 估计 的值在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间4. 一次函数 的图象过点 , , ,则( )A、 B、 C、 D、5. 如图,在 中, ,垂足为D, 与 关于直线AD对称,点的B对称点是 ,则 的度数是( )
3. 估计 的值在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间4. 一次函数 的图象过点 , , ,则( )A、 B、 C、 D、5. 如图,在 中, ,垂足为D, 与 关于直线AD对称,点的B对称点是 ,则 的度数是( )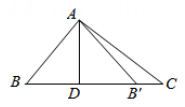 A、 B、 C、 D、6. 等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )A、55°,55° B、70°,40°或70°,55° C、70°,40° D、55°,55°或70°,40°7. 如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A、 B、 C、 D、6. 等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )A、55°,55° B、70°,40°或70°,55° C、70°,40° D、55°,55°或70°,40°7. 如图,若△ABC≌△ADE,则下列结论中一定成立的是( )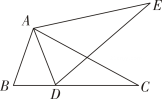 A、AC=DE B、∠BAD=∠CAE C、AB=AE D、∠ABC=∠AED8. 如图是A,B,C三岛的平面图,C岛在A岛的北偏东35度方向,B岛在A岛的北偏东80度方向,C岛在B岛的北偏西55度方向,则A,B,C三岛组成一个( )
A、AC=DE B、∠BAD=∠CAE C、AB=AE D、∠ABC=∠AED8. 如图是A,B,C三岛的平面图,C岛在A岛的北偏东35度方向,B岛在A岛的北偏东80度方向,C岛在B岛的北偏西55度方向,则A,B,C三岛组成一个( )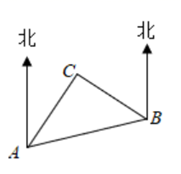 A、等腰直角三角形 B、等腰三角形 C、直角三角形 D、等边三角形9. 在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是( )A、
A、等腰直角三角形 B、等腰三角形 C、直角三角形 D、等边三角形9. 在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是( )A、 B、
B、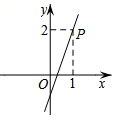 C、
C、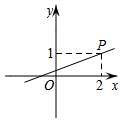 D、
D、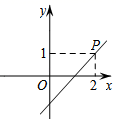 10. 在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=﹣2x交于点A、B,则△AOB的面积为( )A、2 B、3 C、4 D、611. 如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若BC=6,AC=5,则△ACE的周长为( )
10. 在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=﹣2x交于点A、B,则△AOB的面积为( )A、2 B、3 C、4 D、611. 如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若BC=6,AC=5,则△ACE的周长为( )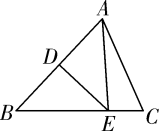 A、8 B、11 C、16 D、1712. 如图, 都是等边三角形,且B,C,D在一条直线上,连结 ,点M,N分别是线段BE,AD上的两点,且 ,则 的形状是( )
A、8 B、11 C、16 D、1712. 如图, 都是等边三角形,且B,C,D在一条直线上,连结 ,点M,N分别是线段BE,AD上的两点,且 ,则 的形状是( )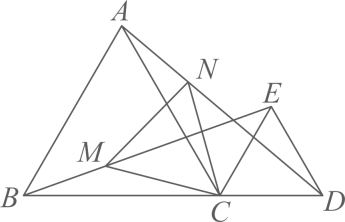 A、等腰三角形 B、直角三角形 C、等边三角形 D、不等边三角形
A、等腰三角形 B、直角三角形 C、等边三角形 D、不等边三角形二、填空题
-
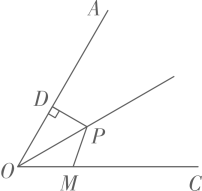
13. 的平方根是 .14. 等腰三角形的两条边长分别为3和4,则这个等腰三角形的周长是 .15. 如图,点P是 的角平分线上一点, ,垂足为点D,且 ,点M是射线 上一动点,则 的最小值为 .
 16. 如图,一个正比例函数图象与一次函数y=-x+1的图象相交于点P,则这个正比例函数的表达式是
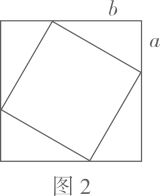
16. 如图,一个正比例函数图象与一次函数y=-x+1的图象相交于点P,则这个正比例函数的表达式是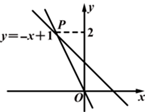 17. 2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1),且大正方形的面积是15,小正方形的面积是3,直角三角形的较短直角边为a,较长直角边为b.如果将四个全等的直角三角形按如图2的形式摆放,那么图2中最大的正方形的面积为.
17. 2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1),且大正方形的面积是15,小正方形的面积是3,直角三角形的较短直角边为a,较长直角边为b.如果将四个全等的直角三角形按如图2的形式摆放,那么图2中最大的正方形的面积为.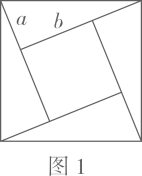
三、解答题
-
18. 计算:(1)、;(2)、 .19. 如图,已知 , , .

求证:
(1)、 ;(2)、 .20. 如图,已知AB=AC,AD=AE,BD和CE相交于点O.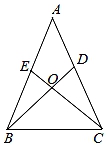 (1)、求证:△ABD≌△ACE;(2)、判断△BOC的形状,并说明理由.21. 如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE.
(1)、求证:△ABD≌△ACE;(2)、判断△BOC的形状,并说明理由.21. 如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE.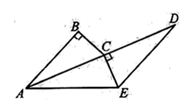 (1)、求证:△ABC≌△DCE;(2)、连结AE,当BC=5,AC=12时,求AE的长.22. 暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
(1)、求证:△ABC≌△DCE;(2)、连结AE,当BC=5,AC=12时,求AE的长.22. 暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠;
设某学生暑期健身x(次),按照方案一所需费用为 ,(元),且 ;按照方案二所需费用为 (元) ,且 其函数图象如图所示.
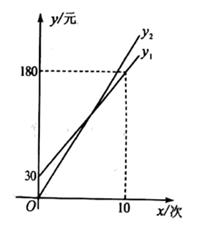 (1)、求 和b的值,并说明它们的实际意义;(2)、求打折前的每次健身费用和 的值;(3)、八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.23. 如图,在 的正方形网格中,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)、求 和b的值,并说明它们的实际意义;(2)、求打折前的每次健身费用和 的值;(3)、八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.23. 如图,在 的正方形网格中,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.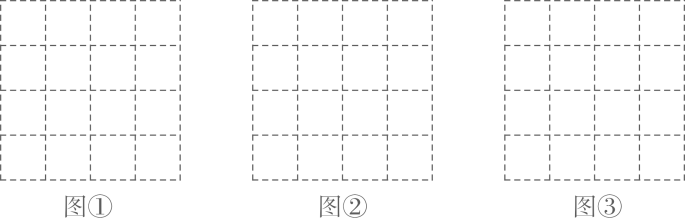 (1)、在图①中,画一个直角三角形,使它的三边长都是有理数;(2)、在图②中,画一个直角三角形,使它的一边长是有理数,另外两边长是无理数;(3)、在图③中,画一个直角三角形,使它的三边长都是无理数.24. 某公司经营甲、乙两种特产,其中甲特产每吨成本价为10万元,销售价为10.5万元;乙特产每吨成本价为1万元,销售价为1.2万元.由于受有关条件限制,该公司每月这两种特产的销售量之和是100吨,且甲特产的销售量都不超过20吨.(1)、若该公司某月销售甲、乙两种特产的总成本为235万元,问这个月该公司分别销售甲、乙两种特产各多少吨?(2)、求该公司一个月销售这两种特产所能获得的最大总利润.
(1)、在图①中,画一个直角三角形,使它的三边长都是有理数;(2)、在图②中,画一个直角三角形,使它的一边长是有理数,另外两边长是无理数;(3)、在图③中,画一个直角三角形,使它的三边长都是无理数.24. 某公司经营甲、乙两种特产,其中甲特产每吨成本价为10万元,销售价为10.5万元;乙特产每吨成本价为1万元,销售价为1.2万元.由于受有关条件限制,该公司每月这两种特产的销售量之和是100吨,且甲特产的销售量都不超过20吨.(1)、若该公司某月销售甲、乙两种特产的总成本为235万元,问这个月该公司分别销售甲、乙两种特产各多少吨?(2)、求该公司一个月销售这两种特产所能获得的最大总利润.