山东省烟台招远市（五四制）2020-2021学年七年级上学期期末数学试题

试卷更新日期：2022-07-20 类型：期末考试

进入出卷网下载

一、单选题

1. 在实数：π， $\sqrt{16}$ ， $\sqrt{3}$ ， 2π， $\sqrt[3]{8}$ ， 0.36，0.3737737773…（相邻两个3之间7的个数逐次加1），﹣ $\frac{7}{22}$ ， $\sqrt{\frac{4}{9}}$ ，无理数的个数为（）

A、4 B、5 C、7 D、9

查看试题解析
2. 下列各曲线中不能表示y是x的函数的是（）

A、 B、 C、 D、

查看试题解析
3. 将一张矩形的纸对折，然后用笔尖在上面扎出“B”，再把它铺平，你可见到（）

A、 B、 C、 D、

查看试题解析
4. 下列判断：①一个数的平方根等于它本身，这个数是 $0$ 和 $1$ ；②实数包括无理数和有理数；③ $2$ 的算术平方根是 $\sqrt{2}$ ；④无理数是带根号的数．正确的有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
5. 如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图，若这个坐标系分别以正东、正北方向为x轴、y轴的正方向，表示太和门的点的坐标为(0，－1)，表示九龙壁的点的坐标为(4，1)，则表示下列宫殿的点的坐标正确的是（）

A、景仁宫(4，2) B、养心殿(－2，3) C、保和殿(1，0) D、武英殿(－3.5，－4)

查看试题解析
6. 已知关于x的方程mx+3=4的解为x=1，则直线y=（m﹣2）x﹣3一定不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 已知点 $P (mn ， m + n)$ 在第四象限，则点 $Q (m ， n)$ 关于x轴对称的点在 $($ 　　 $)$

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 若用我们数学课本上采用的科学计算器进行计算，其按键顺序如图，则输出结果应为（）

A、8 B、4 C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
9. 如图，在 $R t Δ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 30 °$ ，以点 $A$ 为圆心，小于 $A C$ 的长为半径作弧，分别交 $A B$ ， $A C$ 于 $M ， N$ 两点；再分别以点 $M ， N$ 为圆心，大于 $\frac{1}{2} M N$ 长为半径作弧，两弧交于点 $P$ ，作射线 $A P$ 交 $B C$ 于点 $D$ .若 $Δ A B C$ 的面积为9，则 $Δ A C D$ 的面积为（）

A、3 B、 $\frac{9}{2}$ C、6 D、 $\frac{15}{2}$

查看试题解析
10. 表示皮球从高处d落下时，弹跳高度b与下落高度d的关系如下表所示：则d与b之间的关系式为（）

下落高度d

…

80

100

150

…

弹跳高度b

…

40

50

75

…

A、b＝d－40 B、b＝ $\frac{d}{2}$ C、b＝d² D、b＝2d

查看试题解析
11. 有一张矩形纸片ABCD，AB=2.5，AD=1.5，将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F（如图），则CF的长为（）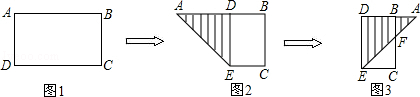

A、1 $\frac{1}{3}$ B、1 C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
12. 一条公路旁依次有A、B、C三个村庄，甲、乙两人骑自行车分别从A村、B村同时出发前往C村，甲、乙之间的距离 $s (k m)$ 与骑行时间 $t (h)$ 之间的函数关系如图所示，下列结论：
①A、B两村相距 $8 k m$ ；
②甲出发 $2 h$ 后到达C村；
③甲每小时比乙我骑行 $8 k m$ ；
④相遇后，乙又骑行了 $15 m i n$ 或 $45 m i n$ 时两人相距 $2 k m$ .
其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. $\sqrt[3]{8}$ 的平方根是．

查看试题解析
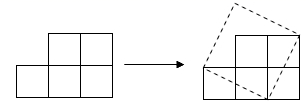
14. 若点A（1＋m，1﹣n）与点B（﹣3，2）关于y轴对称，则（m＋n）²⁰²⁰的值是．

查看试题解析
15. 如果点P在x轴下方，到x轴的距离是5，到y轴的距离是2，那么点P的坐标为

查看试题解析
16. 纸上有五个边长为1的小正方形组成的图形，如图所示，我们可以把它剪开拼成一个正方形．则拼成的正方形的边长为．

查看试题解析
17. 某汽车生产厂对其生产的A型汽车进行油耗试验，试验中汽车为匀速行驶，在行驶过程中，油箱的余油量y（升）与行驶时间t（小时）之间的关系如表：

t（小时）

0

1

2

3

y（升）

120

112

104

96

由表格中y与t的关系可知，当汽车行驶小时，油箱的余油量为0．

查看试题解析
18. 小明将一张正方形纸片按如图所示顺序折叠成纸飞机，当机翼展开在同一平面时(机翼间无缝隙)， $∠ A O B$ 的度数是.

查看试题解析

三、解答题

19. 计算：

(1)、﹣1²+ $\sqrt[3]{- 27}$ ﹣（﹣2）× $\sqrt{9}$

(2)、 $\sqrt{3}$ （ $\sqrt{3}$ +1）+| $\sqrt{3}$ ﹣2|

查看试题解析
20. 如图，在12×10的正方形网格中，△ABC是格点三角形，点B的坐标为（﹣5，1），点C的坐标为（﹣4，5）．
⑴请在方格纸中画出x轴、y轴，并标出原点O；
⑵画出△ABC关于直线l对称的△A₁B₁C₁；C₁的坐标为 ▲
⑶若点P（a，b）在△ABC内，其关于直线l的对称点是P₁ ，则P₁的坐标是 ▲　．

查看试题解析
21. 科学研究发现，空气含氧量y(克/立方米)与海拔高度x(米)之间近似地满足一次函数关系．经测量，在海拔高度为0米的地方，空气含氧量约为299克/立方米；在海拔高度为2000米的地方，空气含氧量约为235克/立方米．

(1)、求出y关于x的函数表达式；

(2)、已知某山的海拔高度为1200米，请你求出该山山顶处的空气含氧量约为多少？

查看试题解析
22. “龟兔赛跑”的故事同学们都非常热悉，图中的线段OD和折线OABC分别表示龟兔赛跑时路程与时间的关系，请你根据图中给出的信息，解决下列问题．

(1)、填空：折线OABC表示赛跑过程中(填“兔子”或“乌龟”)的路程与时间的关系，赛跑的全过程是米．

(2)、兔子在起初每分钟跑多少米？乌龟每分钟爬多少米？

(3)、乌龟用了多少分钟追上了正在睡觉的兔子？

(4)、兔子醒来后，以400米/分的速度跑向终点，结果还是比乌龟晚到了1分钟，请你算算兔子中间停下睡觉用了多少分钟．

查看试题解析
23. 如图，在平面直角坐标系xOy中，一次函数y＝kx＋b的图象与x轴交于点A，与y轴交于点B（0，3），且与正比例函数y＝ $\frac{3}{2}$ x的图象交于点C（m，6）．

(1)、求一次函数y＝kx＋b的函数关系式；

(2)、求△AOC的面积；

(3)、若点M在第二象限，△MAB是以AB为直角边的等腰直角三角形，直接写出点M的坐标．

查看试题解析
24. 已知△ACB和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°

(1)、若D为△ACB内部一点，如图，AE＝BD吗？说明理由

(2)、若D为AB边上一点，AD＝5，BD＝12，求DE的长

查看试题解析
25. 如图， $l_{1}$ 表示振华商场一天的某型电脑销售额与销售量的关系， $l_{2}$ 表示该商场一天的销售成本与电脑销售量的关系．观察图象，解决以下问题：

(1)、当销售量x＝2时，销售额＝万元，销售成本＝万元；

(2)、一天销售台时，销售额等于销售成本；当销售量时，该商场实现赢利（收入大于成本）；

(3)、分别求出 $l_{1}$ 和 $l_{2}$ 对应的函数表达式；

(4)、直接写出利润w与销售量x之间的函数表达式，并求出当销售量x是多少时，每天的利润达到5万元？

查看试题解析

下落高度d	…	80	100	150	…
弹跳高度b	…	40	50	75	…

t（小时）	0	1	2	3
y（升）	120	112	104	96