山东省烟台市莱州市2020-2021学年七年级上学期期末数学试题
试卷更新日期:2022-07-20 类型:期末考试
一、单选题
-
1. 下列各数中,为无理数的是( )A、 B、 C、 D、2. 下列数据能确定物体具体位置的是( )A、明华小区东 B、希望路右边 C、东经118°,北纬28° D、北偏东30°3. 下列图象中,不表示y是x的函数的是( )A、
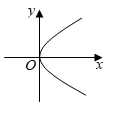 B、
B、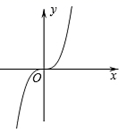 C、
C、 D、
D、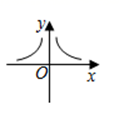 4. 下列各组条件中,不能判定 的是( )A、 B、 C、 D、5. 化简 的结果正确的是( )A、 B、 C、 D、6. 已知点P的坐标是(3,-1),则点P关于x轴的对称点坐标在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图所示的图案是由两个直角三角形和三个正方形组成的图形,其中一直角三角形的斜边和一直角边长分别是13,12,则阴影部分的面积是( )
4. 下列各组条件中,不能判定 的是( )A、 B、 C、 D、5. 化简 的结果正确的是( )A、 B、 C、 D、6. 已知点P的坐标是(3,-1),则点P关于x轴的对称点坐标在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图所示的图案是由两个直角三角形和三个正方形组成的图形,其中一直角三角形的斜边和一直角边长分别是13,12,则阴影部分的面积是( ) A、25 B、16 C、50 D、418. 正比例函数 ( )的函数值y随x的增大而减小,则一次函数 的图象大致是( )A、
A、25 B、16 C、50 D、418. 正比例函数 ( )的函数值y随x的增大而减小,则一次函数 的图象大致是( )A、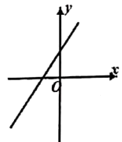 B、
B、 C、
C、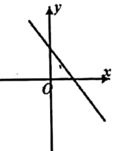 D、
D、 9. 如图,正方形 的边长为2,动点 从点 出发,在正方形的边上沿 的方向运动到点 停止,设点 的运动路程为 ,在下列图象中,能表示 的面积 关于 的函数关系的图象是( )
9. 如图,正方形 的边长为2,动点 从点 出发,在正方形的边上沿 的方向运动到点 停止,设点 的运动路程为 ,在下列图象中,能表示 的面积 关于 的函数关系的图象是( )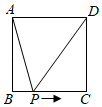 A、
A、 B、
B、 C、
C、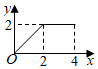 D、
D、 10. 把一张正方形纸片如图①、图②对折两次后,再如图③挖去一个三角形小孔,则展开后图形是( )
10. 把一张正方形纸片如图①、图②对折两次后,再如图③挖去一个三角形小孔,则展开后图形是( )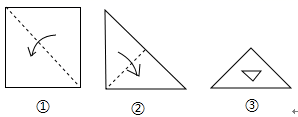 A、
A、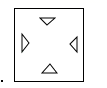 B、
B、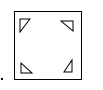 C、
C、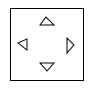 D、
D、
二、填空题
-
11. -64的立方根是 。12. 一次函数 的图象过点 ,将函数 的图象向下平移5个单位长度,所得图象的函数表达式为 .13. 若一个正数的两个不同的平方根为2m﹣6与m+3,则这个正数为14. 函数 是一次函数,则 .15. 已知点 在直线 上,则a= .16. 点A的坐标为 ,以点A为圆心,5个单位长度为半径画圆,与y轴的交点坐标为 .17. 如图, 中, 是 的垂直平分线, , 的周长为 , 则 的周长为 .
 18. 如图,已知点 和 都在直线 上,比较大小: .
18. 如图,已知点 和 都在直线 上,比较大小: . 19. 如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要cm.
19. 如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要cm.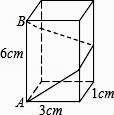 20. 若用初中数学课本上使用的科学计算器进行计算,则以下按键的结果为 .
20. 若用初中数学课本上使用的科学计算器进行计算,则以下按键的结果为 . 21. 已知点 .
21. 已知点 .⑴若点P在y轴上,P点的坐标为 .
⑵若点P的纵坐标比横坐标大6,则点P在第象限.
⑶若点P在过点且与x轴平行的直线上,则点P的坐标为 .
⑷点P到x轴、y轴的距离相等,则点P的坐标为 .
三、解答题
-
22. 计算: .23. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).

⑴请在如图所示的网格平面内作出平面直角坐标系;
⑵请作出△ABC关于y轴对称的△A′B′C′;
⑶写出点B′的坐标.
24. 如图,方格纸中每个小方格的边长为1,在方格纸内作一个面积为5的等腰直角三角形. 25. 若 都是实数,且 ,求 x+3y的立方根。26. 如图,在 中, . 和 的平分线相交于点F, 交 于点D, 交 于点E.求 的周长.
25. 若 都是实数,且 ,求 x+3y的立方根。26. 如图,在 中, . 和 的平分线相交于点F, 交 于点D, 交 于点E.求 的周长. 27. 如图,在平面直角坐标系中,一次函数 与x轴交于点A,与y轴交于点 ,与正比例函数 交于点 .
27. 如图,在平面直角坐标系中,一次函数 与x轴交于点A,与y轴交于点 ,与正比例函数 交于点 . (1)、求直线 的函数表达式;(2)、点P是直线 上的一点,若 的面积为4,求点P的坐标.28. 如图,在 中, , ,D是 的中点, 交 于点G,E为线段 上任意一点,点F在线段 上,且 ,连结 与 ,过点F作 ,交直线 于点H.
(1)、求直线 的函数表达式;(2)、点P是直线 上的一点,若 的面积为4,求点P的坐标.28. 如图,在 中, , ,D是 的中点, 交 于点G,E为线段 上任意一点,点F在线段 上,且 ,连结 与 ,过点F作 ,交直线 于点H. (1)、试说明 的理由;(2)、判断 与 的数量关系,并说明理由.29. 甲、乙两人计划8:00一起从学校出发,乘坐班车去博物馆参观,乙乘坐班车准时出发,但甲临时有事没赶上班车,8:45甲沿相同的路线自行驾车前往,结果比乙早1小时到达.甲、乙两人离学校的距离y(千米)与甲出发时间x(小时)的函数关系如图所示.
(1)、试说明 的理由;(2)、判断 与 的数量关系,并说明理由.29. 甲、乙两人计划8:00一起从学校出发,乘坐班车去博物馆参观,乙乘坐班车准时出发,但甲临时有事没赶上班车,8:45甲沿相同的路线自行驾车前往,结果比乙早1小时到达.甲、乙两人离学校的距离y(千米)与甲出发时间x(小时)的函数关系如图所示. (1)、点A的实际意义是什么?(2)、求甲、乙两人的速度;(3)、求OC和BD的函数关系式;(4)、求学校和博物馆之间的距离.
(1)、点A的实际意义是什么?(2)、求甲、乙两人的速度;(3)、求OC和BD的函数关系式;(4)、求学校和博物馆之间的距离.