山东省烟台市福山区2020-2021学年七年级上学期期末数学试题
试卷更新日期:2022-07-20 类型:期末考试
一、单选题
-
1. 下列实数中,是无理数的是( )A、 B、 C、 D、2. 下列关于数字变换的图案中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算,错误的是( )A、 B、 C、 D、4. 将△ABC各顶点的横坐标都乘以﹣1,纵坐标不变,顺次连接这三个点,得到另一个三角形,下列选项正确的是( )A、
3. 下列计算,错误的是( )A、 B、 C、 D、4. 将△ABC各顶点的横坐标都乘以﹣1,纵坐标不变,顺次连接这三个点,得到另一个三角形,下列选项正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 在平面直角坐标系中,将点 向上平移3个单位长度,再向左平移2个单位长度,得到点 ,则点 的坐标是( ).A、 B、 C、 D、6. 用直角三角板作△ABC的高,下列作法正确的是( )A、
5. 在平面直角坐标系中,将点 向上平移3个单位长度,再向左平移2个单位长度,得到点 ,则点 的坐标是( ).A、 B、 C、 D、6. 用直角三角板作△ABC的高,下列作法正确的是( )A、 B、
B、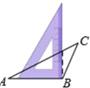 C、
C、 D、
D、 7. 如图所示,若用我们数学课本上采用的科学计算器进行计算,其按键顺序如下:
7. 如图所示,若用我们数学课本上采用的科学计算器进行计算,其按键顺序如下: 按键的结为m:
按键的结为m: 为n,则下列结果判断正确的是( ).
为n,则下列结果判断正确的是( ).
 A、m=n B、 C、m<n D、无法确定8. 如图,用64个边长为的小正方形拼成的网格中,点A,B,C,D,E,都在格点(小正方形顶点)上,对于线段 , , , , 长度为无理数的有( ).
A、m=n B、 C、m<n D、无法确定8. 如图,用64个边长为的小正方形拼成的网格中,点A,B,C,D,E,都在格点(小正方形顶点)上,对于线段 , , , , 长度为无理数的有( ). A、4条 B、3条 C、2条 D、1条9. 直线和在同一平面直角坐标系内的大致图象为( ).A、
A、4条 B、3条 C、2条 D、1条9. 直线和在同一平面直角坐标系内的大致图象为( ).A、 B、
B、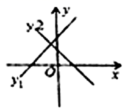 C、
C、 D、
D、 10. 如图,在平面直角坐标系中, 的斜边OA在第一象限,并与x轴的正半轴夹角为30度,C为OA的中点,BC=1,则A点的坐标为( )
10. 如图,在平面直角坐标系中, 的斜边OA在第一象限,并与x轴的正半轴夹角为30度,C为OA的中点,BC=1,则A点的坐标为( )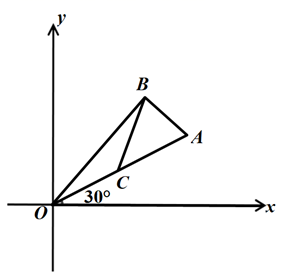 A、 B、 C、 D、11. 如图,正方形 的边长为2,动点 从点 出发,在正方形的边上沿 的方向运动到点 停止,设点 的运动路程为 ,在下列图象中,能表示 的面积 关于 的函数关系的图象是( )
A、 B、 C、 D、11. 如图,正方形 的边长为2,动点 从点 出发,在正方形的边上沿 的方向运动到点 停止,设点 的运动路程为 ,在下列图象中,能表示 的面积 关于 的函数关系的图象是( )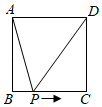 A、
A、 B、
B、 C、
C、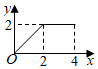 D、
D、 12. 甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )
12. 甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )①甲车的速度为50km/h ②乙车用了3h到达B城
③甲车出发4h时,乙车追上甲车 ④乙车出发后经过1h或3h两车相距50km.
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 若x是16的算术平方根,y是的立方根,则的值为 .14. 在平面直角坐标系中,若点在第三象限,则点在第象限.15. 如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F是AD的三等分点,若△ABC的面积为12cm2 , 则图中阴影部分的面积是 cm2 .
 16. 如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在D′处,若AB=3,AD=4,则S△CED′:S△CEA= .
16. 如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在D′处,若AB=3,AD=4,则S△CED′:S△CEA= .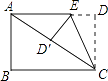 17. 如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形.则原来的纸带宽为。
17. 如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形.则原来的纸带宽为。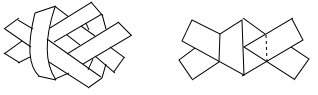 18. 如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是 .
18. 如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是 .
三、解答题
-
19. 计算:(1)、(2)、(3)、20. 如图,一只蚂蚁从点A沿数轴向右爬个单位长度后到达点B,点A表示的数是 , 设点B所表示的数为m.
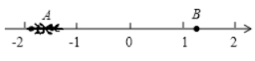 (1)、求m的值;(2)、求的值.21. 已知,如图,AB=AE,AB∥DE,∠ECB=70°,∠D=110°,求证:△ABC≌△EAD.
(1)、求m的值;(2)、求的值.21. 已知,如图,AB=AE,AB∥DE,∠ECB=70°,∠D=110°,求证:△ABC≌△EAD.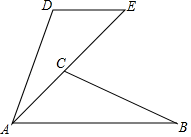 22. 在如图所示的直角坐标系中,A,B,C,D都是网格中的格点(即网线的交点).
22. 在如图所示的直角坐标系中,A,B,C,D都是网格中的格点(即网线的交点). (1)、写出点B与点C的坐标;(2)、若将点B与点C的横坐标保持不变,纵坐标分别乘 , 对应点分别为F,E,连接 , , , 则六边形有什么特点?23. 如图,在中, , 是的垂直平分线,交于点D,交于点E.
(1)、写出点B与点C的坐标;(2)、若将点B与点C的横坐标保持不变,纵坐标分别乘 , 对应点分别为F,E,连接 , , , 则六边形有什么特点?23. 如图,在中, , 是的垂直平分线,交于点D,交于点E. (1)、若 , 求的度数.(2)、若 , , 以点B为坐标原点,分别以、所在的直线为x轴、y轴建立平面直角坐标系,求此时点E的坐标及直线的函数解析式.24. 如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量 (千瓦时)关于已行驶路程 (千米)的函数图象.
(1)、若 , 求的度数.(2)、若 , , 以点B为坐标原点,分别以、所在的直线为x轴、y轴建立平面直角坐标系,求此时点E的坐标及直线的函数解析式.24. 如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量 (千瓦时)关于已行驶路程 (千米)的函数图象.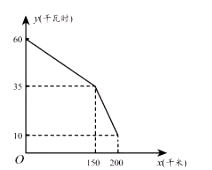 (1)、根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程,当 时,求1千瓦时的电量汽车能行驶的路程;(2)、当 时求 关于 的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.25. 如图,是等边三角形,D是上一点, , .
(1)、根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程,当 时,求1千瓦时的电量汽车能行驶的路程;(2)、当 时求 关于 的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.25. 如图,是等边三角形,D是上一点, , . (1)、试判断与的位置关系,并证明你的结论.(2)、当时,分析与两线段有怎样的数量关系?并说明理由.26. 小华端午节从家里出发,沿笔直道路匀速步行去妈妈经营的商店帮忙,妈妈同时骑三轮车从商店出发,沿相同路线匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5分钟.在此过程中,设妈妈从商店出发开始所用时间为t(分钟),图1表示两人之间的距离s(米)与时间t(分钟)的函数关系的图象;图2中线段 表示小华和商店的距离 (米)与时间t(分钟)的函数关系的图象的一部分,请根据所给信息解答下列问题:
(1)、试判断与的位置关系,并证明你的结论.(2)、当时,分析与两线段有怎样的数量关系?并说明理由.26. 小华端午节从家里出发,沿笔直道路匀速步行去妈妈经营的商店帮忙,妈妈同时骑三轮车从商店出发,沿相同路线匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5分钟.在此过程中,设妈妈从商店出发开始所用时间为t(分钟),图1表示两人之间的距离s(米)与时间t(分钟)的函数关系的图象;图2中线段 表示小华和商店的距离 (米)与时间t(分钟)的函数关系的图象的一部分,请根据所给信息解答下列问题: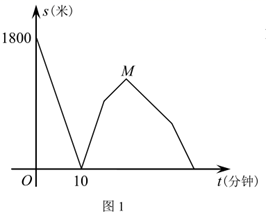
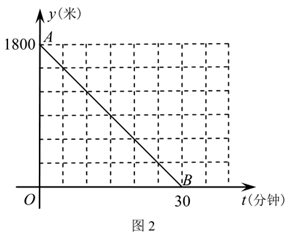 (1)、填空:妈妈骑车的速度是米/分钟,妈妈在家装载货物所用时间是分钟,点M的坐标是;(2)、直接写出妈妈和商店的距离 (米)与时间t(分钟)的函数关系式,并在图2中画出其函数图象;(3)、求t为何值时,两人相距360米.
(1)、填空:妈妈骑车的速度是米/分钟,妈妈在家装载货物所用时间是分钟,点M的坐标是;(2)、直接写出妈妈和商店的距离 (米)与时间t(分钟)的函数关系式,并在图2中画出其函数图象;(3)、求t为何值时,两人相距360米.