山东省潍坊市安丘市2020-2021学年七年级上学期期末数学试题

试卷更新日期：2022-07-20 类型：期末考试

进入出卷网下载

一、单选题

1. $- 2021$ 的倒数的绝对值为（）

A、 $- 2021$ B、 $- \frac{1}{2021}$ C、2021 D、 $\frac{1}{2021}$

查看试题解析
2. 据媒体报道，我国因环境污染造成的巨大经济损失，每年高达680000000元，这个数用科学记数法表示正确的是（）

A、6.8×10⁹元 B、6.8×10⁸元 C、6.8×10⁷元 D、6.8×10⁶元

查看试题解析
3. 下列各组数中，数值相等的是（）

A、 $3^{2}$ 和 $2^{3}$ B、 $(- 2)^{3}$ 和 $- 2^{3}$ C、 $- 3^{2}$ 和 $(- 3)^{2}$ D、 $- (- 2)$ 和 $- | - 2 |$

查看试题解析
4. 已知 $- 2 m^{6} n$ 与 $5^{x} m^{2 x} n^{y}$ 是同类项，则（）

A、x=2，y=1 B、x=3，y=1 C、x= $\frac{3}{2}$ ，y=1 D、x=3，y=0

查看试题解析
5. 已知： $x - 2 y = 3$ ；那么代数式 $x - 2 y - 2 (y - x) - (x - 3)$ 的值为（）

A、3 B、-3 C、6 D、9

查看试题解析
6. 方程 $2 x + a - 4 = 0$ 的解是 $x = - 2$ ，则a等于（）

A、 $- 8$ B、0 C、2 D、8

查看试题解析
7. 一家商店将某型号空调先按原价提高 $20 %$ ，然后广告中写上“大酬宾，九折优惠”，结果被工商部门发现有欺诈行为，为此按每台所得利润的 $10$ 倍处以 $2000$ 元的罚款，则每台空调原价为（）

A、 $1550$ 元 B、 $2000$ 元 C、 $2500$ 元 D、 $2850$ 元

查看试题解析
8. 有一个数值转换器，原理如图所示，若开始输入x的值是5，可发现第1次输出的结果是16，第2次输出的结果是8，第3次输出的结果是4，依次继续下去，第2021次输出的结果是（）

A、1 B、2 C、4 D、8

查看试题解析
9. 已知点 $A$ 、 $B$ 、 $P$ 在一条直线上，则下列等式中，能判断 $P$ 是线段 $A B$ 的中点的是（）

A、 $A P = B P$ B、 $B P = \frac{1}{2} A B$ C、 $A B = 2 A P$ D、 $A P + P B = A B$

查看试题解析
10. 已知数 $a ， b ， c$ 的大小关系如图所示，下列选项中正确的有（）个
① $a b c > 0$ ② $a + b - c > 0$ ③ $\frac{a}{| a |} + \frac{b}{| b |} + \frac{| c |}{c} = 1$ ④ $| a - b | - | c + a | + | b - c | = - 2 a$

A、0 B、1 C、2 D、3

查看试题解析
11. 在大课间活动中，同学们积极参加体育锻炼．小丽在全校随机抽取一部分同学就“一分钟跳绳”进行测试，并以测试数据为样本绘制如图所示的部分条形统计图（从左到右依次分为六个小组，每小组含最小值，不含最大值）和扇形统计图，若“一分钟跳绳”次数不低于130次的成绩为优秀，全校共有1200名学生，根据图中提供的信息，下列说法错误的是（）

A、第四小组有10人 B、第五小组对应圆心角的度数为45° C、本次抽样调查的样本容量为50 D、该校“一分钟跳绳”成绩优秀的人数约为480人

查看试题解析
12. 根据等式的性质，下列变形正确的是（）

A、若 $a = b$ ，则 $a - x = b - y$ B、若 $a = b$ ，则 $\frac{a}{x^{2} + 1} = \frac{b}{x^{2} + 1}$ C、若 $a x = b x$ ，则 $a = b$ D、若 $4 a = 7 b$ ，则 $\frac{a}{4} = \frac{b}{7}$

查看试题解析

二、填空题

13. 多项式 $3 x^{2} - 2 x y^{2} - 1$ 的最高次项是．

查看试题解析
14. 将一个直角三角形ABC绕它的一边旋转，旋转后所得的几何体可能是下面图中的哪个．

查看试题解析
15. 若 $| x - 1 | + {(y + 2)}^{2} = 0$ ，则 ${(x + y)}^{2021} =$ ．

查看试题解析
16. 生物工作者为了估计一片山林中麻雀的数量，设计了如下方案：先捕捉200只麻雀，给它们做上标记后放回山林，一段时间后，再从中随机捕捉300只，其中有标记的麻雀有8只，请帮助工作人员估计这片山林中麻雀的数量约为只．

查看试题解析
17. 若单项式 $\frac{1}{2} x^{2} y^{a}$ 与 $- 2 x^{b} y^{3}$ 的和仍为单项式，则 $a + b =$ ．

查看试题解析
18. 按照如图所示的平面展开图折叠成正方体后，相对面上的两个数都为互为相反数，那么a+2c﹣b＝．

查看试题解析
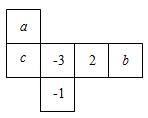19. 对于任意有理数a、b，定义一种新运算“⊕”，规则如下：a⊕b=ab+(a﹣b)，例如：3⊕2=3×2+(3﹣2)=7，则(﹣4)⊕5= ．

查看试题解析
20. 用“●”“■”“▲”分别表示三种不同的物体，如图所示，前两架天平保持平衡，若要使第三架天平也平衡，那么“？”处应放“■”个．

查看试题解析
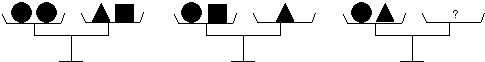21. 观察下列等式： $7^{0} = 1$ ， $7^{1} = 7$ ， $7^{2} = 49$ ， $7^{3} = 343$ ， $7^{4} = 2401$ ， $7^{5} = 16807$ ，…，根据其中的规律可得 $7^{0} + 7^{1} + 7^{2} + \dots + 7^{2021}$ 的结果的个位数字是．

查看试题解析
22. 若（x+p）（x+q）=x²+mx+6，且p，q为整数，则使等式成立的所有m的值为

查看试题解析

三、解答题

23. 计算：

(1)、 $- 5 \times (- 3 \frac{4}{7}) + (- 9) \times 3 \frac{4}{7} + 17 \times (- 3 \frac{4}{7})$

(2)、 $- 1^{4} - (1 - 9) \div | - 4 | \times [3 - {(- 3)}^{2}]$

查看试题解析
24.

(1)、解方程 $\frac{3 x - 1}{4} - \frac{5 x - 7}{6} = 1$

(2)、先化简，再求值： $\frac{1}{2} x - 2 (x - y^{2}) + (- \frac{3}{2} x + \frac{1}{3} y^{2})$ ，其中 $x = - \frac{2}{3}$ ， $y = 3$

查看试题解析
25. 一辆出租车从超市（ $O$ 点）出发，向东走 $2 k m$ 到达小李家（ $A$ 点），继续向东走 $4 k m$ 到达小张家（ $B$ 点），然后又回头向西走 $10 k m$ 到达小陈家（ $C$ 点），最后回到超市．

(1)、以超市为原点，向东方向为正方向，用 $1 c m$ 表示 $1 k m$ ，画出数轴，并在该数轴上表示 $A$ 、 $B$ 、 $C$ 、 $O$ 的位置；

(2)、小陈家（ $C$ 点）距小李家（ $A$ 点）有多远？

(3)、若出租车收费标准如下， $3 k m$ 以内包括 $3 k m$ 收费 $10$ 元，超过 $3 k m$ 部分按每千米 $3$ 元收费，则从超市出发到回到超市一共花费多少元？

查看试题解析
26. 已知关于x的方程 $\frac{x - m}{2} = x + \frac{m}{3}$ 与方程 $\frac{x - 1}{2} = 3 x - 2$ 的解互为倒数，求 $m^{2} - 2 m - 3$ 的值．

查看试题解析
27. 小颖为妈妈准备了一份生日礼物，礼物外包装盒为长方体形状，长、宽、高分别为 $a$ 、 $b$ 、 $c$ $(a > b > c)$ ，为了美观，小颖决定在包装盒外用丝带打包装饰，她发现，可以用如图所示的三种打包方式，所需丝带的长度分别为 $l_{1}$ ， $l_{2}$ ， $l_{3}$ （不计打结处丝带长度）

(1)、用含a、b、c的代数式分别表示 $l_{1}$ ， $l_{2}$ ， $l_{3}$ ；

(2)、方法简介：
要比较两数 $A$ 与 $B$ 大小，我们可以将 $A$ 与 $B$ 作差，结果可能出现三种情况：

① $A - B > 0$ ，则 $A > B$ ；

② $A - B = 0$ ，则 $A = B$ ；

③ $A - B < 0$ ，则 $A < B$ ；

我们将这种比较大小的方法叫做“作差法”．

请帮小颖选出最节省丝带的打包方式，并说明理由．

查看试题解析
28. 某市组织学术研讨会，需租用客车接送参会人员往返宾馆和观摩地点，客车租赁公司现有45座和60座两种型号的客车可供租用．

(1)、已知60座的客车每辆每天的租金比45座的贵100元，会务组第一天在这家公司租了2辆60座和5辆45座的客车．一天的租金为1600元，求45座和60座的客车每辆每天的租金各是多少元？

(2)、由于第二天参会人员发生了变化，因此会务纽需重新确定租车方案．
方案1：若只租用 $45$ 座的客车，会有一辆客车空出30个座位；

方案2：若只租用60座客车，正好坐满且比只租用 $45$ 座的客车少用两辆．

①请计算方案1、2的费用；

②从经济角度考虑，还有方案3吗？如果你是会务纽负责人，应如何确定最终租车方案，并说明理由．

查看试题解析