山东省泰安市东平县(五四制)2020-2021学年七年级上学期期末考试数学试题
试卷更新日期:2022-07-20 类型:期末考试
一、单选题
-
1. 如图,下列图形中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各式中,正确的是( )A、 B、 C、 D、3. 下列说法正确的是( )A、全等三角形是指形状相同的两个三角形 B、全等三角形的周长和面积分别相等 C、全等三角形是指面积相等的两个三角形 D、所有的等边三角形都是全等三角形4. 在平面直角坐标系中,点(﹣1,m2+1)一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 根据下列条件,能判定△ABC≌△DEF的是( )A、AB=DE,BC=EF,∠A=∠D B、∠A=∠D,∠C=∠F,AC=EF C、∠B=∠E,∠A=∠D,AC=EF D、AB=DE,BC=EF,∠B=∠E6. 如图,在 中, , .若 是 的高,与角平分线 相交于点 ,则 的度数为( )
2. 下列各式中,正确的是( )A、 B、 C、 D、3. 下列说法正确的是( )A、全等三角形是指形状相同的两个三角形 B、全等三角形的周长和面积分别相等 C、全等三角形是指面积相等的两个三角形 D、所有的等边三角形都是全等三角形4. 在平面直角坐标系中,点(﹣1,m2+1)一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 根据下列条件,能判定△ABC≌△DEF的是( )A、AB=DE,BC=EF,∠A=∠D B、∠A=∠D,∠C=∠F,AC=EF C、∠B=∠E,∠A=∠D,AC=EF D、AB=DE,BC=EF,∠B=∠E6. 如图,在 中, , .若 是 的高,与角平分线 相交于点 ,则 的度数为( )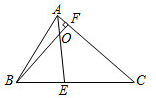 A、130° B、70° C、110° D、100°7. 在下列四组线段中,能组成直角三角形的是( )A、a=32 , b=42 , c=52 B、a=11,b=12,c=13 C、a=9,b=40,c=41 D、a:b:c=1:1:28. 已知一次函数y=kx+b随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )A、
A、130° B、70° C、110° D、100°7. 在下列四组线段中,能组成直角三角形的是( )A、a=32 , b=42 , c=52 B、a=11,b=12,c=13 C、a=9,b=40,c=41 D、a:b:c=1:1:28. 已知一次函数y=kx+b随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )A、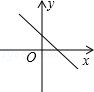 B、
B、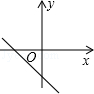 C、
C、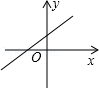 D、
D、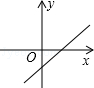 9. 下列叙述中错误的一项是( )A、三角形的中线、角平分线、高都是线段 B、三角形的三条高线中至少存在一条在三角形内部 C、只有一条高在三角形内部的三角形一定是钝角三角形 D、三角形的三条角平分线都在三角形内部10. 已知A、B两点的坐标分别是和 , 则下面四个结论:①A、B关于x轴对称;②A、B关于y轴对称;③A、B关于原点对称;④A、B之间的距离为4,其中正确的有( )A、1个 B、2个 C、3个 D、4个11. 下列在具体情境中不能确定平面内位置的是( )A、东经37°,北纬21° B、电影院某放映厅7排3号 C、东平县贯中大道 D、烟台山灯塔北偏东60°方向,距离灯塔3千米12. 已知直线不经过第二象限,也不经过原点,则下列结论正确的是( )A、 , B、 , C、 , D、 ,13. 潜山市某村办工厂,今年前5个月生产某种产品的总量C(件)关于时间t(月)的函数图象如图所示,则该厂对这种产品来说( )
9. 下列叙述中错误的一项是( )A、三角形的中线、角平分线、高都是线段 B、三角形的三条高线中至少存在一条在三角形内部 C、只有一条高在三角形内部的三角形一定是钝角三角形 D、三角形的三条角平分线都在三角形内部10. 已知A、B两点的坐标分别是和 , 则下面四个结论:①A、B关于x轴对称;②A、B关于y轴对称;③A、B关于原点对称;④A、B之间的距离为4,其中正确的有( )A、1个 B、2个 C、3个 D、4个11. 下列在具体情境中不能确定平面内位置的是( )A、东经37°,北纬21° B、电影院某放映厅7排3号 C、东平县贯中大道 D、烟台山灯塔北偏东60°方向,距离灯塔3千米12. 已知直线不经过第二象限,也不经过原点,则下列结论正确的是( )A、 , B、 , C、 , D、 ,13. 潜山市某村办工厂,今年前5个月生产某种产品的总量C(件)关于时间t(月)的函数图象如图所示,则该厂对这种产品来说( )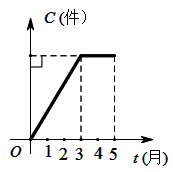 A、1月至3月每月生产总量逐月增加,4、5两月每月生产总量逐月减少 B、1月至3月每月生产总量逐月增加,4,5两月每月生产量与3月持平 C、1月至3月每月生产总量逐月增加,4、5两月均停止生产 D、1月至3月每月生产总量不变,4、5两月均停止生产14. 如图,中, , D是的中点,的垂直平分线分别交 , , 于点E,O,F,则图中全等三角形的对数是( )
A、1月至3月每月生产总量逐月增加,4、5两月每月生产总量逐月减少 B、1月至3月每月生产总量逐月增加,4,5两月每月生产量与3月持平 C、1月至3月每月生产总量逐月增加,4、5两月均停止生产 D、1月至3月每月生产总量不变,4、5两月均停止生产14. 如图,中, , D是的中点,的垂直平分线分别交 , , 于点E,O,F,则图中全等三角形的对数是( )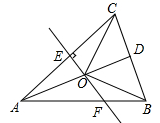 A、对 B、对 C、对 D、对
A、对 B、对 C、对 D、对二、填空题
-
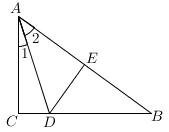
15. 在中, , , 则°.16. 若 , 则 .17. 如图,在中, , 垂直平分 , 交于E,交于 , , 则°.
 18. 含45 直角三角板如图放置在平面直角坐标系中,其中A(-2,0)、B(0,1),则直线BC的解析式为 .
18. 含45 直角三角板如图放置在平面直角坐标系中,其中A(-2,0)、B(0,1),则直线BC的解析式为 .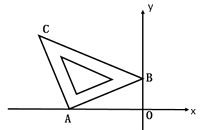 19. 已知点P的坐标为 , 则点P到原点的距离为 .20. 如果函数的图像经过点 , 则它经过x轴上的点的坐标为 .21. 如图,等边 的边长为 ,D、E分别是 、 上的点,将 沿直线 折叠,点A落在点F处,且点F在 外部,则阴影部分图形的周长为cm.
19. 已知点P的坐标为 , 则点P到原点的距离为 .20. 如果函数的图像经过点 , 则它经过x轴上的点的坐标为 .21. 如图,等边 的边长为 ,D、E分别是 、 上的点,将 沿直线 折叠,点A落在点F处,且点F在 外部,则阴影部分图形的周长为cm.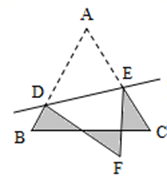 22. 在平面直角坐标系中,若干个边长为1个单位长度的等边三角形,按如图中的规律摆放.点P从原点O出发,以每秒1个单位长度的速度沿着等边三角形的边“”的路线运动,设第n秒运动到点(n为正整数),则点的坐标是 .
22. 在平面直角坐标系中,若干个边长为1个单位长度的等边三角形,按如图中的规律摆放.点P从原点O出发,以每秒1个单位长度的速度沿着等边三角形的边“”的路线运动,设第n秒运动到点(n为正整数),则点的坐标是 .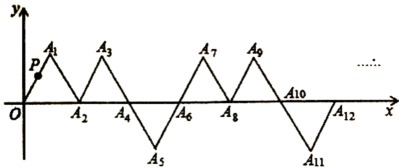
三、解答题
-
23. 计算(1)、(2)、24. 如图,四边形ABCD中,AB=3,BC=4,CD=13,AD=12,∠B=90°,求四边形ABCD的面积.
 25. 如图, , , , .
25. 如图, , , , .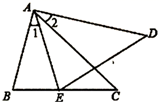 (1)、试说明: ;(2)、求 的度数.26. 如图,已知直线L1经过点A(﹣1,0)与点B(2,3),另一条直线L2经过点B,且与x轴相交于点P(m,0).
(1)、试说明: ;(2)、求 的度数.26. 如图,已知直线L1经过点A(﹣1,0)与点B(2,3),另一条直线L2经过点B,且与x轴相交于点P(m,0).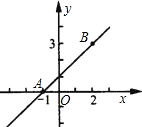 (1)、求直线L1的解析式.(2)、若△APB的面积为3,求m的值.(提示:分两种情形,即点P在A的左侧和右侧)
(1)、求直线L1的解析式.(2)、若△APB的面积为3,求m的值.(提示:分两种情形,即点P在A的左侧和右侧)
