山东省日照市岚山区2020-2021学年七年级上学期期末数学试题
试卷更新日期:2022-07-20 类型:期末考试
一、单选题
-
1. 在 , 0,−π,|-2.5|,0.333, , 这7个数中,正有理数的个数是( )A、3个 B、4个 C、5个 D、6个2. 如图,数轴上有A,B,C,D四个点,其中绝对值最小的数对应的点是( )
 A、点A B、点B C、点C D、点D3. 在算式中的所在位置,填入下列运算符号,能使最后计算出来的值最小的符号是( )A、+ B、− C、× D、÷4. 在式子2abc,π, , , , 中,单项式的个数是( )A、2个 B、3个 C、4个 D、5个5. 下列运算正确的是( )A、 B、 C、 D、6. 下列说法错误的是( )A、5.80万是精确到百位的近似数 B、近似数58.3与58.30表示的意义不相同 C、2.7×104精确到十分位 D、近似数2.20是由数a四舍五入得到的,那么数a的取值范围是7. 如图,小明同学用剪刀沿着虚线将一张圆形纸片剪掉一部分,发现剩下纸片的周长比原来的周长要小,能符合题意解释这一现象的数学知识是( )
A、点A B、点B C、点C D、点D3. 在算式中的所在位置,填入下列运算符号,能使最后计算出来的值最小的符号是( )A、+ B、− C、× D、÷4. 在式子2abc,π, , , , 中,单项式的个数是( )A、2个 B、3个 C、4个 D、5个5. 下列运算正确的是( )A、 B、 C、 D、6. 下列说法错误的是( )A、5.80万是精确到百位的近似数 B、近似数58.3与58.30表示的意义不相同 C、2.7×104精确到十分位 D、近似数2.20是由数a四舍五入得到的,那么数a的取值范围是7. 如图,小明同学用剪刀沿着虚线将一张圆形纸片剪掉一部分,发现剩下纸片的周长比原来的周长要小,能符合题意解释这一现象的数学知识是( )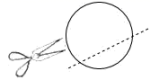 A、两点之间,直线最短 B、经过一点,有无数条直线 C、两点确定一条直线 D、两点之间,线段最短8. 下列图形都是由六个相同的正方形组成的,经过折叠不能围成正方体的是( )A、
A、两点之间,直线最短 B、经过一点,有无数条直线 C、两点确定一条直线 D、两点之间,线段最短8. 下列图形都是由六个相同的正方形组成的,经过折叠不能围成正方体的是( )A、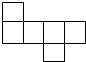 B、
B、 C、
C、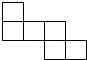 D、
D、 9. 一个角的补角比这个角的余角的2倍还多40°,则这个角的度数是( )A、40° B、50° C、60° D、70°10. 已知−2是关于x的一元一次方程ax+b=1的解,则代数式的值是( )A、0 B、1 C、2 D、311. 如图,已知∠AOB=120°,从∠AOB的内部引两条射线OM、ON,使得夹角∠MON=60°,则∠AON与∠BOM一定满足的关系是( )
9. 一个角的补角比这个角的余角的2倍还多40°,则这个角的度数是( )A、40° B、50° C、60° D、70°10. 已知−2是关于x的一元一次方程ax+b=1的解,则代数式的值是( )A、0 B、1 C、2 D、311. 如图,已知∠AOB=120°,从∠AOB的内部引两条射线OM、ON,使得夹角∠MON=60°,则∠AON与∠BOM一定满足的关系是( ) A、∠AON+∠BOM=120° B、∠AON+∠BOM=180° C、∠AON=∠BOM D、∠AON=2∠BOM12. 一套仪器由1个A部件和3个B部件构成,1立方米钢材可做40个A部件或240个B部件,现要用6立方米钢材制作这种仪器,设应用x立方米钢材做B部件,其他钢材做A部件,恰好配套,则可列方程为( )A、 B、 C、 D、
A、∠AON+∠BOM=120° B、∠AON+∠BOM=180° C、∠AON=∠BOM D、∠AON=2∠BOM12. 一套仪器由1个A部件和3个B部件构成,1立方米钢材可做40个A部件或240个B部件,现要用6立方米钢材制作这种仪器,设应用x立方米钢材做B部件,其他钢材做A部件,恰好配套,则可列方程为( )A、 B、 C、 D、二、填空题
-
13. 国家统计局2020年12月10日公布的全国粮食生产数据显示,我国粮食生产实现“十七连丰”:2020年全国粮食总产量为13390亿斤,产量连续6年保持在1.3万亿斤以上.将“13390亿”用科学记数法表示为 .14. 计算= .15. 如图,B、C为线段AD上的两点,若线段AD的长度为a,线段BC的长度为b,则图中所有线段的长度之和为 .
 16. 如图,小悦和小萱同学一起玩“数字盒子”的游戏:先任意想一个数输入“数字盒子”中,按顺序进行四次运算后,得到一个输出的数.若小悦想了一个数,并告诉小萱这个数经过 “数字盒子”后输出的数是−2,则小悦所想的数是 .
16. 如图,小悦和小萱同学一起玩“数字盒子”的游戏:先任意想一个数输入“数字盒子”中,按顺序进行四次运算后,得到一个输出的数.若小悦想了一个数,并告诉小萱这个数经过 “数字盒子”后输出的数是−2,则小悦所想的数是 .
三、解答题
-
17.(1)、计算:(2)、先化简,再求值: , 其中18. 如图,已知正方形网格中的三点A,B,C,按下列要求完成画图和解答:
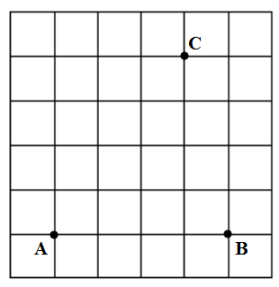
⑴画线段AB,画射线AC,画直线BC ;
⑵取AB的中点D,并连接CD;
⑶根据图形可以看出:∠ ▲ 与∠ ▲ 互为补角.
19. 数学课上老师布置大家解方程 , 小星同学板演的解题过程如下:(解析)解:去分母,得
. ①
去括号,得
. ②
移项,得
. ③
合并同类项,得
. ④
系数化为1,得
. ⑤
(1)、老师批阅后说小星同学的解题过程有误,你认为出现错误的步骤是(只填写序号),错误原因是: , 这个方程正确的解应该是x= .然后,请你自己细心解下面的方程:
(2)、 .20. 如图1,点A、O、B在同一条直线上,∠BOC=40°,OD平分∠AOC.从点O出发画一条射线OE,使得∠COE=90°.请画出满足条件的射线OE,并求出∠DOE的度数.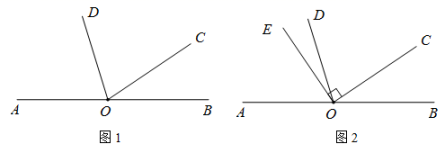 (1)、如图2,已画出射线OE的第一种位置,请将解题过程补充完整:
(1)、如图2,已画出射线OE的第一种位置,请将解题过程补充完整:(解析)解:因为∠AOB=180°,∠BOC=40°,
所以∠AOC=∠−∠=°.
因为OD平分∠AOC,
所以∠COD=∠=°.
因为∠COE=90°,
所以∠DOE=∠−∠=°.
(2)、请在图3中画出射线OE的第二种位置,并直接写出此种情况下∠DOE的度数.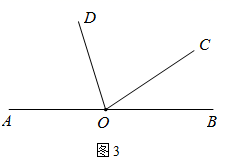 21. 阅读下面的材料,解决有关问题:
21. 阅读下面的材料,解决有关问题:在如图1的“数表”中,数字按一定规律排列,我们分别在“数表”中涂抹出两个“H”,在每个“H”所覆盖的7个数字中,将最上端两数的和与最下端两数的和相减,计算结果称为“H值”.

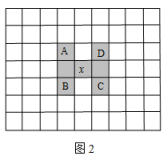 (1)、(计算与发现)分别计算图1中的两个不同位置的“H”所对应的“H值”:(2+4)−(20+22)=;(24+26)−(42+44)= , 我们可以初步发现:;(2)、(探究与证明)图2是从图1中截出的一部分,在“H”所覆盖的7个数字中,若设中心数为x,则A、B、C、D所对应的数可分别表示为 , , , .(用含x的代数式表示),并请你利用整式的运算,对(计算与发现)中发现的规律进行验证 .22. 疫情期间,某蛋糕店采用“线上”销售模式,即提前一天线上下单,第二天无接触送货上门.为了吸引客户,在A、B两种蛋糕送达时,采用赠代金券的返利方式给顾客意外惊喜.已知返利方式有两种,每种方式返利后A、B两种蛋糕的实际利润如下表:
(1)、(计算与发现)分别计算图1中的两个不同位置的“H”所对应的“H值”:(2+4)−(20+22)=;(24+26)−(42+44)= , 我们可以初步发现:;(2)、(探究与证明)图2是从图1中截出的一部分,在“H”所覆盖的7个数字中,若设中心数为x,则A、B、C、D所对应的数可分别表示为 , , , .(用含x的代数式表示),并请你利用整式的运算,对(计算与发现)中发现的规律进行验证 .22. 疫情期间,某蛋糕店采用“线上”销售模式,即提前一天线上下单,第二天无接触送货上门.为了吸引客户,在A、B两种蛋糕送达时,采用赠代金券的返利方式给顾客意外惊喜.已知返利方式有两种,每种方式返利后A、B两种蛋糕的实际利润如下表:方案
A种蛋糕每盒实际利润(元)
B种蛋糕每盒实际利润(元)
方式一
10
8
方式二
9
11
蛋糕店每日限量销售A、B两种蛋糕共计30盒,且都能售完,每天只推出一种返利方式.
(1)、若采用方式一返利,某天销售A、B两种蛋糕的实际利润共274元,则A、B两种蛋糕各售出多少盒?(2)、下完订单的当晚,店员M说:“明天无论采用哪种返利方式,销售A、B两种蛋糕的实际总利润都一样”,你觉得她的判断会成立吗?请说明理由.