山东省临沂市沂水县2020-2021学年七年级上学期期末数学试题
试卷更新日期:2022-07-20 类型:期末考试
一、单选题
-
1. 的相反数是( )A、 B、 C、3 D、-32. 下面的图形经过折叠可以围成一个棱柱的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列方程中,是一元一次方程的是( )A、x﹣y=2 B、y2﹣y=2 C、3y=2 D、=24. 高速公路的建设带动我国经济的快速发展.在高速公路的建设中,通常要从大山中开挖隧道穿过,把道路取直,以缩短路程.这样做包含的数学道理是( )A、两点确定一条直线 B、两点之间,线段最短 C、两条直线相交,只有一个交点 D、直线是向两个方向无限延伸的5. 下列各式正确的是( )A、﹣|﹣|= B、﹣(﹣)=﹣ C、|﹣|=﹣ D、﹣(﹣)=6. 下列说法正确的是( )A、m2+m﹣1的常数项为1 B、单项式32mn3的次数是6次 C、多项式的次数是1,项数是2 D、单项式﹣πmn的系数是﹣7. 下列等式的变形,正确的是( )A、若x2=5x,则x=5 B、若m+n=2n,则m=n C、若=(b≠0,d≠0),则a=c,b=d D、若x=y,则=8. 如图,已知三点A,B,C画直线AB,画射线AC,连接BC,按照上述语句画图正确的是( )A、
3. 下列方程中,是一元一次方程的是( )A、x﹣y=2 B、y2﹣y=2 C、3y=2 D、=24. 高速公路的建设带动我国经济的快速发展.在高速公路的建设中,通常要从大山中开挖隧道穿过,把道路取直,以缩短路程.这样做包含的数学道理是( )A、两点确定一条直线 B、两点之间,线段最短 C、两条直线相交,只有一个交点 D、直线是向两个方向无限延伸的5. 下列各式正确的是( )A、﹣|﹣|= B、﹣(﹣)=﹣ C、|﹣|=﹣ D、﹣(﹣)=6. 下列说法正确的是( )A、m2+m﹣1的常数项为1 B、单项式32mn3的次数是6次 C、多项式的次数是1,项数是2 D、单项式﹣πmn的系数是﹣7. 下列等式的变形,正确的是( )A、若x2=5x,则x=5 B、若m+n=2n,则m=n C、若=(b≠0,d≠0),则a=c,b=d D、若x=y,则=8. 如图,已知三点A,B,C画直线AB,画射线AC,连接BC,按照上述语句画图正确的是( )A、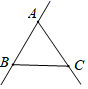 B、
B、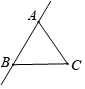 C、
C、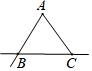 D、
D、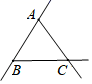 9. 如果代数式﹣3xa+3y2与xyb﹣1是同类项,那么ab的值是( )A、5 B、8 C、﹣8 D、﹣510. 若关于x的一元一次方程2k﹣x﹣4=0的解是x=﹣3,那么k的值是( )A、 B、 C、6 D、1011. 用一副三角板拼成的图形如图所示,其中B,C,D三点在同一条直线上.则图中∠ACE的大小为( )
9. 如果代数式﹣3xa+3y2与xyb﹣1是同类项,那么ab的值是( )A、5 B、8 C、﹣8 D、﹣510. 若关于x的一元一次方程2k﹣x﹣4=0的解是x=﹣3,那么k的值是( )A、 B、 C、6 D、1011. 用一副三角板拼成的图形如图所示,其中B,C,D三点在同一条直线上.则图中∠ACE的大小为( )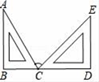 A、45° B、60° C、75° D、105°12. 在数轴上,点M,N在原点O的两侧,分别表示数m,2,将点M向右平移1个单位长度,得到点P,若PO=NO,则m的值为( )A、1 B、﹣1 C、﹣2 D、﹣313. 如图,A地和B地都是海上观测站,B地在A地正东方向,从A地发现它的北偏东60°方向有一艘船C,同时,从B地发现船C在它的北偏东30°方向,此时在C船上观测A,B两地.下列说法正确的是( )
A、45° B、60° C、75° D、105°12. 在数轴上,点M,N在原点O的两侧,分别表示数m,2,将点M向右平移1个单位长度,得到点P,若PO=NO,则m的值为( )A、1 B、﹣1 C、﹣2 D、﹣313. 如图,A地和B地都是海上观测站,B地在A地正东方向,从A地发现它的北偏东60°方向有一艘船C,同时,从B地发现船C在它的北偏东30°方向,此时在C船上观测A,B两地.下列说法正确的是( ) A、A地在C船南偏西30°方向 B、A地在C船北偏西60°方向 C、B地在C船南偏西30°方向 D、B地在C船北偏西60°方向14. 《九章算术》是我国古代的第一 部自成体系的数学专著, 其中的许多数学问题是世界上记载最早的,《九章算术》卷七“盈不足”有如下记载: 原文:今有共买璡①,人出半,盈四;人出少半,不足三。问人数、进价各几何?
A、A地在C船南偏西30°方向 B、A地在C船北偏西60°方向 C、B地在C船南偏西30°方向 D、B地在C船北偏西60°方向14. 《九章算术》是我国古代的第一 部自成体系的数学专著, 其中的许多数学问题是世界上记载最早的,《九章算术》卷七“盈不足”有如下记载: 原文:今有共买璡①,人出半,盈四;人出少半,不足三。问人数、进价各几何?注释:①璡jin:像玉的石头.
译文:今有人合伙买璡石,每人出钱,会多钱;每人出钱,又差钱,问人数璡价各是多少?设璡价是x钱,则依题意有( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
15. 用“>”或“<”符号填空:﹣﹣ .16. 化简的结果为 .17. 如图的框图表示了琳琳同学解方程+1=的流程,你认为琳琳同学在解这个方程的过程中从第步开始出现问题,正确完成这一步的依据是 .
 18. 如图,点O在直线AB上,OC是∠AOD的平分线,若∠AOC=65°,则∠BOD的度数为 .
18. 如图,点O在直线AB上,OC是∠AOD的平分线,若∠AOC=65°,则∠BOD的度数为 . 19. 某商场在“庆元旦”的活动中将某种服装打折销售,如果每件服装按标价的5折出售将亏30元,而按标价的8折出售将赚30元,则每件服装的进价是元.
19. 某商场在“庆元旦”的活动中将某种服装打折销售,如果每件服装按标价的5折出售将亏30元,而按标价的8折出售将赚30元,则每件服装的进价是元.三、解答题
-
20. 计算:(1)、(﹣2)+(﹣3)﹣(+1)﹣(﹣6);(2)、﹣22﹣(﹣2)2×0.25÷;(3)、(3x﹣2)﹣(x﹣3);(4)、5﹣2(a2b﹣ab2)+(3a2b+ab2).21. 解方程:(1)、(2)、22. 某健身馆推出两种健身付费方式.方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证健身每次再付费5元;方式二:不购买会员证,每次健身付费9元.什么情况下,购会员证与不购证付一样的钱?23. 已知:点P是线段MN上的点,PM=2,点Q是线段PN的中点,PQ=4.画出图形,并求线段MN的长.24. 如图,已知∠AOB=130°,画∠AOB的平分线OC,画射线OD,使∠COD和∠AOC互余,并求∠BOD的度数.
 25. 某玩具厂生产某种玩具,A组的4名工人一天生产的总件数比每人每天任务量的3倍多20件,B组的5名工人一天生产的总件数比每人每天任务量的5倍少20件.(1)、如果两组工人一天人均生产件数相等,那么每人每天任务量是多少件?(2)、如果A组工人一天人均生产件数比B组的多2件,则每人每天任务量是多少件?(3)、如果A组工人一天人均生产件数比B组的少2件,则每人每天任务量是多少件?26.
25. 某玩具厂生产某种玩具,A组的4名工人一天生产的总件数比每人每天任务量的3倍多20件,B组的5名工人一天生产的总件数比每人每天任务量的5倍少20件.(1)、如果两组工人一天人均生产件数相等,那么每人每天任务量是多少件?(2)、如果A组工人一天人均生产件数比B组的多2件,则每人每天任务量是多少件?(3)、如果A组工人一天人均生产件数比B组的少2件,则每人每天任务量是多少件?26. (1)、已知图①中的三角形ABC,分别作AB,BC,CA的延长线BD,CE,AF,测量∠CBD,∠ACE,∠BAF的度数,并计算∠CBD+∠ACE+∠BAF.由此你有什么发现?请利用所学知识解释说明;(2)、类似地,已知图②中的四边形PQRS,分别作PQ,QR,RS,SP的延长线QG,RH,SM,PN,测量∠RQG,∠SRH,∠PSM,∠QPN的度数,并计算∠RQG+∠SRH+∠PSM+∠QPN.由此你又有什么发现?(3)、综合(1)(2)的发现,你还能进一步得到什么猜想?
(1)、已知图①中的三角形ABC,分别作AB,BC,CA的延长线BD,CE,AF,测量∠CBD,∠ACE,∠BAF的度数,并计算∠CBD+∠ACE+∠BAF.由此你有什么发现?请利用所学知识解释说明;(2)、类似地,已知图②中的四边形PQRS,分别作PQ,QR,RS,SP的延长线QG,RH,SM,PN,测量∠RQG,∠SRH,∠PSM,∠QPN的度数,并计算∠RQG+∠SRH+∠PSM+∠QPN.由此你又有什么发现?(3)、综合(1)(2)的发现,你还能进一步得到什么猜想?