山东省临沂市沂南县2020-2021学年七年级上学期期末数学试题

试卷更新日期：2022-07-20 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣|﹣2021|等于（）

A、﹣2021 B、2021 C、﹣ $\frac{1}{2021}$ D、 $\frac{1}{2021}$

查看试题解析
2. 如图，射线 $O A$ 表示的方向是（）

A、北偏东 $65 °$ B、北偏西 $35 °$ C、南偏东 $65 °$ D、南偏西 $35 °$

查看试题解析
3. 下列各组中的单项式是同类项的是（　　）

A、﹣m²np和﹣mn² B、2xy²和﹣ $\frac{1}{2}$ y²x C、﹣m²和﹣2m D、0.5a 和﹣ $\frac{1}{2}$ b

查看试题解析
4. 如图的几何体由5个相同的小正方体搭成，从正面看，这个几何体的形状是（）

A、 B、 C、 D、

查看试题解析
5. 在数轴上，到表示-5的点的距离等于5个单位的点所表示的数是（）

A、10 B、 $- 10$ C、0或 $- 10$ D、 $- 10$ 或10

查看试题解析
6. 如果3m=3n，那么下列等式不一定成立的是（　　）

A、m-3=n-3 B、3m+3=3n+2 C、5+m=5+n D、 $\frac{m}{- 3}$ = $\frac{n}{- 3}$

查看试题解析
7. 方程 $\frac{1}{2} x - \frac{5 x + 3}{7} = 1$ ，去分母得（）

A、 $7 x - 10 x + 6 = 1$ B、 $7 x - 10 x - 6 = 14$ C、 $7 x - 10 x - 6 = 1$ D、 $7 x - 5 x + 60 = 14$

查看试题解析
8. 如图，是一个小正方体的展开图，把展开图折叠成小正方体后，有“新”字一面的相对面上的字是（）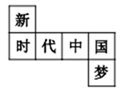

A、代 B、中 C、国 D、梦

查看试题解析
9. 若代数式3x+2与2互为相反数，则x的值为（）

A、2 B、﹣2 C、0 D、 $- \frac{4}{3}$

查看试题解析
10. 已知∠1和∠2互为余角，且∠2与∠3互补，∠1＝60°，则∠3为（）

A、120° B、60° C、30° D、150°

查看试题解析
11. 《九章算术》是我国古代的数学专著，卷七“盈不足”中有这样一题：“今有共买鸡，人出九，盈十一；人出六，不足十六．问人数、鸡价各几何？”题目大意是：有几个人共同出钱买鸡，每人出钱9，则多了钱11，每人出钱6，则少了钱16，那么有几人共同买鸡？鸡的价钱是多少？设有x人共同买鸡，根据题意，可列方程为（　　）

A、 $\frac{x + 11}{9} = \frac{x - 16}{6}$ B、 $\frac{x - 11}{9} = \frac{x + 16}{6}$ C、9x﹣11＝6x+16 D、9x+11＝6x﹣16

查看试题解析
12. 如图，已知C为线段 $A D$ 上一点，点B为 $C D$ 的中点，且 $A D = 9 ， B D = 2$ ．若点E在直线 $A D$ 上，且 $E A = 1$ ，则 $B E$ 的长为（）

A、4 B、6或8 C、6 D、8

查看试题解析

二、填空题

13. 比﹣2℃高6℃的温度是℃．

查看试题解析
14. 列式表示“比x的平方的2倍大3的数”：．

查看试题解析
15. 若2x﹣y＝﹣1，则7+4x﹣2y的值是．

查看试题解析
16. 若关于x的方程9+ax=3的解是x=-2，则a的值是．

查看试题解析
17. 如图，∠AOC＝90°，OC平分∠DOB，且∠DOC＝22°39′，∠BOA度数是．

查看试题解析
18. 有如下定义：数轴上有三个点，若其中一个点与其它两个点的距离恰好满足3倍的数量关系，则称该点是其它两个点的“关键点”．若点A表示数﹣4，点B表示数8，M为数轴一个动点．若点M在线段AB上，且点M是点A、点B的“关键点”，则此时点M表示的数是．

查看试题解析

三、解答题

19. 计算题

(1)、（﹣5）﹣（﹣10）+（﹣32）﹣（﹣7）；

(2)、﹣1¹⁰+|2﹣（﹣3）²|+ $\frac{1}{2}$ ÷（﹣ $\frac{3}{2}$ ）．

查看试题解析
20. 解方程： $\frac{2 x + 1}{3} - \frac{x - 1}{5}$ ＝1．

查看试题解析
21. 如图，点A，O，B在同一条直线上，OD、OE分别平分∠AOC和∠BOC．

(1)、求∠DOE的度数；

(2)、如果∠COD＝70°，求∠AOE的度数．

查看试题解析
22. 已知A＝3x²+y²﹣2xy ， B＝xy﹣y²+2x² ，求：

(1)、2A﹣3B；

(2)、若|x+2|+（y﹣3）²＝0，求2A﹣3B的值．

查看试题解析
23. 已知线段m、n．

(1)、尺规作图：作线段AB，满足AB＝m+n（保留作图痕迹，不用写作法）；

(2)、在（1）的条件下，点O是AB的中点，点C在线段AB上，且满足AC＝m，当m＝5，n＝3时，求线段OC的长．

查看试题解析
24. 某水果销售店用1000元购进甲、乙两种新出产的水果共140千克，这两种水果的进价、售价如表所示：

进价

（元/千克）

售价

（元/千克）

甲种

5

8

乙种

9

13

(1)、这两种水果各购进多少千克?

(2)、若该水果店按售价销售完这批水果，获得的利润是多少元?

查看试题解析
25. 已知O为直线AB上一点，将一直角三角板OMN的直角顶点放在点O处．射线OC平分∠MOB．

(1)、如图1，若∠AOM＝30°，求∠CON的度数；

(2)、在图1中，若∠AOM＝ $α$ ，直接写出∠CON的度数（用含 $α$ 的代数式表示）；

(3)、将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置，当∠AOC＝3∠BON时，求∠AOM的度数．

查看试题解析