山东省临沂市临沭县2020-2021学年七年级上学期期末数学试题
试卷更新日期:2022-07-20 类型:期末考试
一、单选题
-
1. 中国人最早使用负数,可追溯到两千多年前的秦汉时期, 的相反数是( )A、 B、 C、 D、2. 2020年6月23日,我国的北斗卫星导航系统(BDS)星座部署完成,其中一颗中高轨道卫星高度大约是21500000米.将数字21500000用科学记数法表示为( )A、 B、 C、 D、3. 单项式的系数为( )A、 B、 C、 D、4. 如图是由6个大小相同的小正方体组成的几何体,从上面看到的是( )
 A、
A、 B、
B、 C、
C、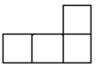 D、
D、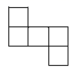 5. 下列各式运用等式的性质变形,错误的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则6. 已知 , , 则与的关系为( )A、相等 B、互余 C、互补 D、以上都不对7. 下列四个生活、生产现象:①用两枚钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③体育课上,老师测量某同学的跳远成绩;④把弯曲的公路改直,就能缩短路程,其中可用基本事实“两点确定一条直线”来解释的现象有( )A、①② B、①③ C、②④ D、③④8. 下列方程的变形,正确的是( )A、由 , 得 B、由 , 得 C、由 , 得 D、由 , 得9. 把一副三角板按如图所示方式拼在一起,并作的平分线 , 则的度数是( )
5. 下列各式运用等式的性质变形,错误的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则6. 已知 , , 则与的关系为( )A、相等 B、互余 C、互补 D、以上都不对7. 下列四个生活、生产现象:①用两枚钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③体育课上,老师测量某同学的跳远成绩;④把弯曲的公路改直,就能缩短路程,其中可用基本事实“两点确定一条直线”来解释的现象有( )A、①② B、①③ C、②④ D、③④8. 下列方程的变形,正确的是( )A、由 , 得 B、由 , 得 C、由 , 得 D、由 , 得9. 把一副三角板按如图所示方式拼在一起,并作的平分线 , 则的度数是( ) A、120° B、60° C、30° D、15°10. 下列叙述中错误的个数是( )
A、120° B、60° C、30° D、15°10. 下列叙述中错误的个数是( )①任何有理数都有倒数;②互为倒数的两个数的积为1;③若 , 则;④若 , 则;⑤若 , 则a,b同号.
A、1个 B、2个 C、3个 D、4个11. 已知线段 ,下面有四个说法: ①线段 长可能为 ;②线段 长可能为 ;③线段 长不可能为 ;④线段 长可能为 .所有正确说法的序号是( )A、①② B、③④ C、①②④ D、①②③④12. 一件夹克衫先按成本提高40%标价,再以七五折(标价的75%)出售,结果仍获利36元,若设这件夹克衫的成本是x元,根据题意,可得到的方程是( )A、(1+40%x)×75%=x-36 B、(1+40%x)×75%=x+36 C、(1+40%)x×75%=x+36 D、(1+40%)x×75%=x-3613. 数学课上,张老师出示了这样一道题目:“当时,求已知的值”.解完这道题后,小茗同学发现:“是多余的条件”.师生讨论后,一致认为小茗的发现是正确的.受此启发,张老师又出示了一道题目:无论取任何值,多项式的值都不变,则系数的值分别为( )A、 B、 C、 D、14. 已知有理数在数轴上的位置如图所示,且满足 . 则下列各式:①;②;③;④ . 其中正确的有( )
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
15.
如图,数轴上的点P表示的数是-1,将点P向右移动3个单位长度得到点P′,则点P′ 表示的数是 .
 16. 若与是同类项,则的值为 .17. 已知直线l上有A、B、C三点,且AB=8cm,BC=3cm,则线段AC=cm.18. 已知关于x的方程的解为 , 则的值为 .19. 历史上数学家欧拉最先把关于 的多项式用记号 来表示,把 等于某数 时的多项式的值用 来表示.例如,对于多项式 ,当 时,多项式的值为 ,若 ,则 的值为.
16. 若与是同类项,则的值为 .17. 已知直线l上有A、B、C三点,且AB=8cm,BC=3cm,则线段AC=cm.18. 已知关于x的方程的解为 , 则的值为 .19. 历史上数学家欧拉最先把关于 的多项式用记号 来表示,把 等于某数 时的多项式的值用 来表示.例如,对于多项式 ,当 时,多项式的值为 ,若 ,则 的值为.三、解答题
-
20. 计算下列各题:(1)、(2)、21. 先化简,再求值: , 其中 .22. 解方程:23. 如图,O为直线上一点, , 平分 , .
 (1)、求出的度数;(2)、试判断是否平分 , 并简要说明理由.24. 如图所示,点C在线段上,点分别是的中点.
(1)、求出的度数;(2)、试判断是否平分 , 并简要说明理由.24. 如图所示,点C在线段上,点分别是的中点. (1)、若cm,cm,求的长;(2)、若cm,其他条件不变,你能猜想出的长度吗?并说明理由;(3)、若点C是线段延长线上一点,且满足cm,其他条件不变,请画出图形,并直接写出的长度.25. 某制药厂制造一批药品,如用旧工艺,则废水排水量要比环保限制的最大量还多200吨;如用新工艺,则废水排水量要比环保限制的最大量少100吨. 新旧工艺的废水排水量之比为2:5,则环保限制的最大量是多少吨?26.(1)、(理解新知)如图①,已知 , 在内部画射线 , 得到三个角分别为 . 若这三个角中有一个角是另外一个角的2倍,则称射线为的“2倍角线”.
(1)、若cm,cm,求的长;(2)、若cm,其他条件不变,你能猜想出的长度吗?并说明理由;(3)、若点C是线段延长线上一点,且满足cm,其他条件不变,请画出图形,并直接写出的长度.25. 某制药厂制造一批药品,如用旧工艺,则废水排水量要比环保限制的最大量还多200吨;如用新工艺,则废水排水量要比环保限制的最大量少100吨. 新旧工艺的废水排水量之比为2:5,则环保限制的最大量是多少吨?26.(1)、(理解新知)如图①,已知 , 在内部画射线 , 得到三个角分别为 . 若这三个角中有一个角是另外一个角的2倍,则称射线为的“2倍角线”.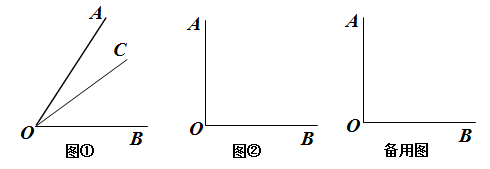
角的平分线(填“是”或“不是”)这个角的“2倍角线”;
(2)、若 , 射线为的“2倍角线”,则= .(3)、(解决问题)如图②,已知 , 射线从从发,以每秒的速度绕O点逆时针旋转;射线从出发,以每秒的速度绕O点顺时针旋转;射线、同时出发,当一条射线回到出发位置的时候,整个运动随之停止,设运动时间为t秒.当射线、旋转到同一条直线上时,求t的值.