山东省临沂市费县2020-2021学年七年级上学期期末数学试题

试卷更新日期：2022-07-20 类型：期末考试

进入出卷网下载

一、单选题

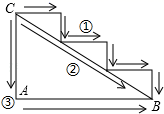
1. 如果水位上升5m时水位变化记为+5m，那么水位下降2m时水位变化记作（　　）

A、+5m B、﹣5m C、+2m D、﹣2m

查看试题解析
2. 如图，从C地到B地有①②③条路线可以走，下列判断正确的是（　　）

A、路线①最短 B、路线②最短 C、路线③最短 D、①②③长度都一样

查看试题解析
3. “扶贫”是新时期党和国家的重点工作之一，为落实习近平总书记提出的“精准扶贫”战略构想，某省预计三年内脱贫1020000人，数字1020000用科学记数法可表示为（）

A、1.02×10⁶ B、1.02×10⁵ C、10.2×10⁵ D、102×10⁴

查看试题解析
4. 下列各组的两个式子是同类项的一组是（）

A、x和y B、3和π C、﹣a²b³和﹣a²b³c D、x²y和xy²

查看试题解析
5. 若 $x = 1$ 是方程 $2 x + a = 0$ 的解，则a的值是（）

A、 $1$ B、 $2$ C、 $- 1$ D、 $- 2$

查看试题解析
6. 下列解方程过程正确的是（　　）

A、2x＝1系数化为1，得x＝2 B、x﹣2＝0解得x＝2 C、3x﹣2＝2x﹣3移项得3x﹣2x＝﹣3﹣2 D、x﹣（3﹣2x）＝2（x+1）去括号得x﹣3﹣2x＝2x+1

查看试题解析
7. 下列说法中，①两条射线组成的图形叫角；②两点之间，直线最短；③同角（或等角）的余角相等；④若AB＝BC，则点B是线段AC的中点；正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，射线 $O A$ 表示的方向是（）

A、北偏东 $65 °$ B、北偏西 $35 °$ C、南偏东 $65 °$ D、南偏西 $35 °$

查看试题解析
9. 2020年是不寻常的一年，病毒无情人有情，很多最美逆行者奔赴疫情的前线，不顾自己的安危令我们感动.文德中学初一年级学习小组送给医务工作者的正方体6面上都有一个汉字，如图所示是它的一种展开图，那么在原正方体中，与“最”字所在面相对的面上的汉字是（）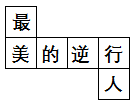

A、美 B、的 C、逆 D、人

查看试题解析
10. 根据等式的性质，下列结论错误的是（　　）

A、若 $a + \frac{m}{2} = b + \frac{m}{2}$ ，则a＝b B、若a﹣3n＝b﹣3n，则a＝b C、若ax＝bx，则a＝b D、若 $\frac{a}{y} = \frac{b}{y}$ ，则a＝b

查看试题解析
11. 一个角的补角加上10°后，等于这个角的余角的3倍，则这个角是（）

A、30° B、35° C、40° D、45°

查看试题解析
12. 一项工程，甲单独做需要5天完成，乙单独做需要8天完成．若甲先做1天，然后由甲、乙合作完成此项工程．求甲一共做了多少天？若设甲一共做了x天，则所列方程为（）

A、 $\frac{x}{5}$ + $\frac{x + 1}{8}$ ＝1 B、 $\frac{x}{5}$ + $\frac{x - 1}{8}$ ＝1 C、 $\frac{x}{5}$ ﹣ $\frac{x + 1}{8}$ ＝1 D、 $\frac{x}{5}$ ﹣ $\frac{x - 1}{8}$ ＝1

查看试题解析
13. 互联网“微商”经营已成为大众创业的新途径，某微信平台将一件商品按进价提高 $40 %$ 后标价，又以八折优惠卖出，结果每件仍获利48元，这种商品每件的进价是多少元？若设每件的进价是x元，那么所列方程为（）

A、 $40 % (1 + 80 %) x - x = 48$ B、 $80 % (1 + 40 %) x - x = 48$ C、 $x - 80 % (1 + 40 %) x = 48$ D、 $80 % (1 - 40 %) x - x = 48$

查看试题解析
14. 定义一种对正整数n的“F运算”：①当n为奇数时，运算结果为3n+5；②当n为偶数时，结果为 $\frac{n}{2^{k}}$ （其中k是使 $\frac{n}{2^{k}}$ 为奇数的正整数），并且运算重复进行，例如，取n＝26，则
若n＝898，则第2021次“F运算”的结果是（　　）

A、488 B、1 C、4 D、8

查看试题解析

二、填空题

15. 若m与-2互为相反数，则m的值为。

查看试题解析
16. 已知，∠A＝46°28'，则∠A的余角＝.

查看试题解析
17. 将一副三角板如图放置，若 $∠ A O D = 20^{\circ}$ ，则 $∠ B O C$ 的大小为．

查看试题解析
18. 已知代数式x﹣2y的值是3，则代数式y+2x+1﹣5y的值是．

查看试题解析
19. 已知线段 $A B = 8 cm$ ，在直线 $A B$ 上画线段 $A C = 5 cm$ ，则 $B C$ 的长是 $cm$ ．

查看试题解析

三、解答题

20. 计算：

(1)、5+（﹣8）﹣（﹣7）+|﹣3|．

(2)、﹣1⁴﹣[2﹣（﹣3）²]÷（ $\frac{1}{2}$ ）³ ．

查看试题解析
21. 解下列方程：

(1)、4x﹣4＝6﹣x；

(2)、 $\frac{x - 1}{2}$ ﹣ $\frac{4 x - 2}{3}$ ＝1．

查看试题解析
22. 如图：已知AB＝8cm，BD＝3cm，C为AB的中点，求线段DC的长．

查看试题解析
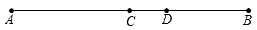23. 已知多项式M＝（2x²+3xy+2y）﹣2（x²﹣x+yx﹣ $\frac{1}{2}$ ）．

(1)、先化简，再求值，其中x＝ $\frac{1}{5}$ ， y＝﹣1；

(2)、若多项式M与字母x的取值无关，求y的值．

查看试题解析
24. 某车间为提高生产总量，在原有16名工人的基础上，新调入若干名工人，使得调整后车间的总人数是调入工人人数的3倍多4人．

(1)、调入多少名工人；

(2)、在（1）的条件下，每名工人每天可以生产1200个螺柱或2000个螺母，1个螺柱需要2个螺母，为使每天生产的螺桩和螺母刚好配套，应该安排生产螺柱和螺母的工人各多少名？

查看试题解析
25. 已知：点 $O$ 为直线 $A B$ 上一点，过点 $O$ 作射线 $O C$ ， $∠ B O C = 100 °$ ．

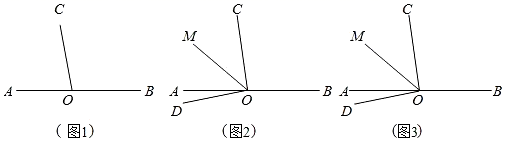(1)、如图1，求 $∠ A O C$ 的度数；

(2)、如图2，过点 $O$ 作射线 $O D$ ，使 $∠ C O D = 90 °$ ，作 $∠ A O C$ 的平分线 $O M$ ，求 $∠ M O D$ 的度数；

(3)、如图3，在（2）的条件下，作射线 $O P$ ，若 $∠ B O P$ 与 $∠ A O M$ 互余，请画出图形，并求 $∠ C O P$ 的度数．

查看试题解析
26. 在“清洁乡村”活动中，某村长提出了两种购买垃圾桶方案．
方案一：买分类垃圾桶，需要费用3000元，以后每月的垃圾处理费用250元；

方案二：买不分类垃圾桶，需要费用1000元，以后每月的垃圾处理费用500元．

设交费时间为x个月，方案一的购买费和垃圾处理费共为M元，方案二的购买费和垃圾处理费共为N元．

(1)、分别用x表示M，N；

(2)、若交费时间为12个月，哪种方案更合适，并说明理由．

(3)、交费时间为多少个月时，两种方案费用相同？

查看试题解析