山东省聊城市莘县2020-2021学年七年级上学期期末数学试题
试卷更新日期:2022-07-20 类型:期末考试
一、单选题
-
1. 某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“我”字所在面相对的面上的汉字是
 A、厉 B、害 C、了 D、国2. 下列说法中错误的是( )A、0既不是正数也不是负数 B、整数包括正整数和负整数 C、非负数包括正数和0 D、整数和分数统称为有理数3. 绝对值不大于3的所有整数的积等于( )A、-36 B、6 C、36 D、04. 某学习小组为了解本城市100万成年人中大约有多少人吸烟,随机调查了50个成年人,结果其中有10个成年人吸烟,对于这个数据收集与处理的问题,下列说法正确的是( )A、该调查的方式是普查 B、本城市只有40个成年人不吸烟 C、本城市一定有20万人吸烟 D、样本容量是505. 如图,若数轴上A,B两点所对应的有理数分别为a,b,则化简的结果为( )
A、厉 B、害 C、了 D、国2. 下列说法中错误的是( )A、0既不是正数也不是负数 B、整数包括正整数和负整数 C、非负数包括正数和0 D、整数和分数统称为有理数3. 绝对值不大于3的所有整数的积等于( )A、-36 B、6 C、36 D、04. 某学习小组为了解本城市100万成年人中大约有多少人吸烟,随机调查了50个成年人,结果其中有10个成年人吸烟,对于这个数据收集与处理的问题,下列说法正确的是( )A、该调查的方式是普查 B、本城市只有40个成年人不吸烟 C、本城市一定有20万人吸烟 D、样本容量是505. 如图,若数轴上A,B两点所对应的有理数分别为a,b,则化简的结果为( ) A、0 B、 C、 D、6. 在2020年11月11日的网上促销活动中,全网总销售额达到3143亿元.其中3143亿元用科学记数法表示为( )A、 B、 C、 D、7. 下列等式变形正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则8. 下列说法正确的是 ( )A、a是代数式,1不是代数式 B、表示a,b,的积的代数式为ab C、的意义是:a与4的差除b的商 D、a,b两数差的平方与a,b两数的积的4倍的和表示为(a-b)2+4ab9. 若关于x,y的多项式化简后不含二次项,则( )A、 B、 C、 D、10. 下列说法中正确的是( )A、单项式 , 它的系数是0.9,次数是0 B、多项式 , 它的系数是4,次数是2 C、一个两位数的个位数上的数是a,十位数上的是b,则这两位数表示为 D、与不是同类项11. 某企业今年3月份产值为a万元,4月份比3月份减少了10%,5月份比4月份增加了15%,则5月份的产值是( )
A、0 B、 C、 D、6. 在2020年11月11日的网上促销活动中,全网总销售额达到3143亿元.其中3143亿元用科学记数法表示为( )A、 B、 C、 D、7. 下列等式变形正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则8. 下列说法正确的是 ( )A、a是代数式,1不是代数式 B、表示a,b,的积的代数式为ab C、的意义是:a与4的差除b的商 D、a,b两数差的平方与a,b两数的积的4倍的和表示为(a-b)2+4ab9. 若关于x,y的多项式化简后不含二次项,则( )A、 B、 C、 D、10. 下列说法中正确的是( )A、单项式 , 它的系数是0.9,次数是0 B、多项式 , 它的系数是4,次数是2 C、一个两位数的个位数上的数是a,十位数上的是b,则这两位数表示为 D、与不是同类项11. 某企业今年3月份产值为a万元,4月份比3月份减少了10%,5月份比4月份增加了15%,则5月份的产值是( )
A、(a-10%)(a+15%)万元 B、a(1-10%)(1+15%)万元 C、(a-10%+15%)万元 D、a(1-10%+15%)万元12. 按图中程序运算,如果输出的结果为3,则输入的数据可能是( )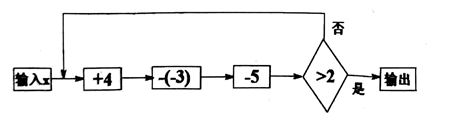 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若关于x的方程是一元一次方程,则m的值为 .14. 单项式与的和仍是单项式,则的值是 .15. 已知 , 那么 .16. 规定*是一种运算符号,且 , 则计算 .17. 我们把分子为1的分数叫做理想分数,如 , , , …,任何一个理想分数都可以写成两个不同理想分数的和,如=+ , =+ , =+ , …,根据对上述式子的观察,请你思考:如果理想分数=+(n是不小于2的整数,且a<b),那么b﹣a=(用含n的式子表示)
三、解答题
-
18. 计算:(1)、(2)、19. 解方程:(1)、(2)、20. 先化简,再求值:2x2y﹣[5xy2+2(x2y﹣3xy2+1)],其中x,y满足(x﹣2)2+|y+1|=0.21. 已知多项式 , , 如果 , 求多项式C.22. 如图,线段AB=8,点C是线段AB的中点,点D是线段BC的中点.
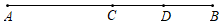 (1)、求线段AD的长;(2)、若在线段AB上有一点E , CE= BC , 求AE的长.23. 一次试验中,小明把一根弹簧的上端固定,在其下端悬挂砝码,下面是测得的弹簧长度与所挂砝码的质量的一组对应值:
(1)、求线段AD的长;(2)、若在线段AB上有一点E , CE= BC , 求AE的长.23. 一次试验中,小明把一根弹簧的上端固定,在其下端悬挂砝码,下面是测得的弹簧长度与所挂砝码的质量的一组对应值:0
1
2
3
4
5
…
18
20
22
24
26
28
…
(1)、表中反映了哪两个变量之间的关系?(2)、弹簧的原长是多少?当所挂砝码质量为时,弹簧的长度是多少?(3)、砝码质量每增加 , 弹簧的长度增加_▲_ .(4)、请写出y与x之间的关系式(写成用含x的式子表示y的形式),并判断y是不是x的函数.24. 某中学开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②所示的统计图,已知“查资料”的人数是40人.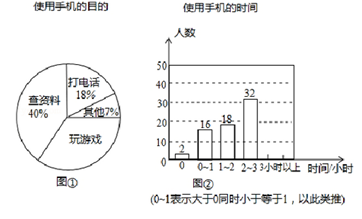
请你根据图中信息解答下列问题:
(1)、在扇形统计图中,“玩游戏”对应的圆心角度数是°;
(2)、补全条形统计图;
(3)、该校共有学生1200人,试估计每周使用手机时间在2小时以上(不含2小时)的人数.
25. 某牛奶加工厂有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获取利润500元,制成酸奶销售,每吨可获取利润1200元;制成奶片销售,每吨可获利润2000元,该工厂的生产能力是:若制成酸奶,每天可加工3吨;制成奶片每天可加工1吨,受人员限制,两种加工方式不可同时进行,受气温条件限制,这批牛奶必须在4天内全部销售或加工完毕.为此,该厂某领导提出了两种可行方案:方案1:尽可能多的制成奶片,其余直接销售鲜牛奶;
方案2:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成.
你认为选择哪种方案获利最多,为什么?