山东省济宁市泗水县2020-2021学年七年级上学期期末数学试题
试卷更新日期:2022-07-20 类型:期末考试
一、单选题
-
1. 在有理数-4,0,-1,3中,最小的数是( )A、-4 B、0 C、-1 D、32. 把弯曲的河道改成直的,可以缩短航程,其理由是( )A、经过两点有且只有一条直线 B、两点之间,线段最短 C、两点之间,直线最短 D、线段可以比较大小3. 据测算,我国每天因土地沙漠化造成的经济损失约为亿元,一年的经济损失约为54750000000元,用科学记数法表示一年的经济损失为( )万元.A、 B、 C、 D、4. 下列图形经过折叠后,不能围成正方体的是( )A、
 B、
B、 C、
C、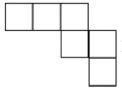 D、
D、 5. 已知和是同类项,则式子的值是( )A、1 B、 C、0 D、6. 若 , , , 则下列结论正确的是( )A、 B、 C、 D、7. 如图,下列说法中错误的是( )
5. 已知和是同类项,则式子的值是( )A、1 B、 C、0 D、6. 若 , , , 则下列结论正确的是( )A、 B、 C、 D、7. 如图,下列说法中错误的是( ) A、OA的方向是东北方向 B、OB的方向是北偏西60° C、OC的方向是南偏西60° D、OD的方向是南偏东60°8. 用一副三角板画角,不能画出的角是 ( )A、15° B、75° C、145° D、165°9. 已知 , 则多项式的值等于( )A、1 B、4 C、-1 D、-410. 如图所示 , , , 若 , 则( )
A、OA的方向是东北方向 B、OB的方向是北偏西60° C、OC的方向是南偏西60° D、OD的方向是南偏东60°8. 用一副三角板画角,不能画出的角是 ( )A、15° B、75° C、145° D、165°9. 已知 , 则多项式的值等于( )A、1 B、4 C、-1 D、-410. 如图所示 , , , 若 , 则( ) A、6cm B、8cm C、10cm D、12cm11. 某车间原计划用13小时生产一批零件,后来每小时多生产10件,用了12小时不但完成了任务,而且还多生产60件.设原计划每小时生产 个零件,则所列方程为( )A、 B、 C、 D、12. 有一数值转换器,原理如图所示.若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,则第2020次输出的结果是( )
A、6cm B、8cm C、10cm D、12cm11. 某车间原计划用13小时生产一批零件,后来每小时多生产10件,用了12小时不但完成了任务,而且还多生产60件.设原计划每小时生产 个零件,则所列方程为( )A、 B、 C、 D、12. 有一数值转换器,原理如图所示.若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,则第2020次输出的结果是( ) A、1 B、2 C、4 D、8
A、1 B、2 C、4 D、8二、填空题
-
13. 若方程 是关于x的一元一次方程,则a等于14. 一副三角板按如图方式摆放,且的度数比的度数大 , 则 .
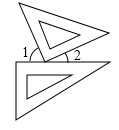 15. 某商品的销售价格每件900元,为了参加市场竞争,商店按售价的九折再让利40元销售,此时仍可获利 , 此商品的进价为元.16. 若a,b互为相反数,c,d互为倒数,且a≠0,则 = .17. 一辆货运小汽车以15米/秒的速度向对面山谷行驶,司机鸣一下喇叭,4秒后听到回响,这时汽车离山谷米(已知空气中声音的传播速度约为340米/秒).18. 瑞士中学教师巴尔末成功的从光谱数据: ,……中得到巴尔末公式,从而打开光谱奥妙的大门.请你根据以上光谱数据的规律写出它的第七个数据.
15. 某商品的销售价格每件900元,为了参加市场竞争,商店按售价的九折再让利40元销售,此时仍可获利 , 此商品的进价为元.16. 若a,b互为相反数,c,d互为倒数,且a≠0,则 = .17. 一辆货运小汽车以15米/秒的速度向对面山谷行驶,司机鸣一下喇叭,4秒后听到回响,这时汽车离山谷米(已知空气中声音的传播速度约为340米/秒).18. 瑞士中学教师巴尔末成功的从光谱数据: ,……中得到巴尔末公式,从而打开光谱奥妙的大门.请你根据以上光谱数据的规律写出它的第七个数据.三、解答题
-
19. 计算或化简(1)、计算(2)、化简20. 解方程:(1)、(2)、21. 先化简,再求值.
, 其中 .
22. 如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线. (1)、如果∠AOB=150°,求∠COE的度数;(2)、如果∠AOB=120°,那么∠COE=;(3)、如果∠AOB=α,那么∠COE= .23. 定义新运算: , , 等式右边是通常的加法、减法运算;(1)、求的值;(2)、化简:;(3)、若 , 求x的值.24. 观察下面的图形(每个正方形的边长均为1)和相应的等式,探究其中的规律:
(1)、如果∠AOB=150°,求∠COE的度数;(2)、如果∠AOB=120°,那么∠COE=;(3)、如果∠AOB=α,那么∠COE= .23. 定义新运算: , , 等式右边是通常的加法、减法运算;(1)、求的值;(2)、化简:;(3)、若 , 求x的值.24. 观察下面的图形(每个正方形的边长均为1)和相应的等式,探究其中的规律:
①
②
③
④
(1)、写出第五个等式,并在右边给出的五个正方形上画出与之对应的图示; (2)、猜想并写出与第n个图形相对应的等式.
(2)、猜想并写出与第n个图形相对应的等式.