山东省济宁市金乡县2020-2021学年七年级上学期期末数学试题

试卷更新日期：2022-07-20 类型：期末考试

进入出卷网下载

一、单选题

1. 化简－(+2)的结果是（）

A、－2 B、2 C、±2 D、0

查看试题解析
2. 据统计，截至2020年6月，中国网民规模达到9.4亿，9.4亿这个数值（）

A、精确到十分位 B、精确到百万位 C、精确到千万位 D、精确到亿位

查看试题解析
3. 已知有理数a，b在数轴上的位置如图所示，则化简代数式|a+b|﹣|a﹣b|的结果是（）

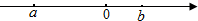A、﹣b B、﹣2b C、a D、2a﹣b

查看试题解析
4. 下列说法正确的是（）

A、 $- \frac{x y^{2}}{5}$ 的系数是 $- 5$ B、单项式 $x$ 的系数为 $1$ ，次数为 $0$ C、 $x y + x$ 次数为 $2$ 次 D、 $- 2^{2} x y z^{2}$ 的系数为 $- 2$

查看试题解析
5. 若方程（k﹣2）x^|k|﹣1+4k＝0是关于x的一元一次方程，则k的值为（）

A、1 B、﹣2 C、2或﹣2 D、2

查看试题解析
6. 下列方程的变形正确的是（）．

A、由 $3 x - 2 = 2 x + 1$ 移项，得 $3 x - 2 x = - 1 + 2$ B、由 $3 - x = 2 - 5 (x - 1)$ 去括号，得 $3 - x = 2 - 5 x - 5$ C、由 $\frac{4}{5} x = - \frac{4}{5}$ 系数化为1，得 $x = 1$ D、由 $\frac{x}{2} - \frac{x - 1}{3} = 3$ 去分母，得 $3 x - 2 (x - 1) = 18$

查看试题解析
7. 定义运算“*”，其规则为 $a * b = \frac{2 a + b}{3}$ ，则方程 $4 * x = 4$ 的解为（）

A、 $x = - 3$ B、 $x = 3$ C、 $x = 2$ D、 $x = 4$

查看试题解析
8. 用度、分、秒表示 $21.24 °$ 为（）

A、 $21 ° 1 4^{'} 2 4^{″}$ B、 $21 ° 2 0^{'} 2 4^{″}$ C、 $21 ° 3 4^{'}$ D、 $21 °$

查看试题解析
9. 某车间有62名工人，生产甲、乙两种零件，每人每天平均能生产甲种零件12个或乙种零件23个，若3个甲种零件和2个乙种零件配成一套，应分配多少人生产甲种零件，多少人生产乙种零件，才能使每天生产的甲种零件和乙种零件刚好配套?设应分配 $x$ 人生产甲种零件，则根据题意可得的方程为（）

A、 $12 x = 62 (23 - x)$ B、 $3 \times 12 x = 2 \times 23 (62 - x)$ C、 $2 \times 12 x = 3 \times 23 (62 - x)$ D、 $\frac{3}{5} \times 23 (62 - x) = 12 x$

查看试题解析
10. 定义一种对正整数n的“F”运算：①当n为奇数时，结果为3n+5；②当n为偶数时，结果为 $\frac{n}{2^{k}}$ ；（其中k是使 $\frac{n}{2^{k}}$ 为奇数的正整数），并且运算可以重复进行，例如，取n=26．则：
若n=49，则第2020次“F运算”的结果是（　）

A、152 B、19 C、62 D、31

查看试题解析

二、填空题

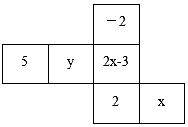
11. 已知：|x|＝3，y²＝4且xy＜0，则（x+y）²⁰¹⁹＝．

查看试题解析
12. 若 $2 x^{3} b^{2 m}$ 与 $- \frac{1}{3} x^{n} b^{4}$ 是同类项，则m+n=.

查看试题解析
13. 如图是一个正方体的平面展开图，正方体中相对的面上的数字或代数式互为相反数，则2x+3y的值为.

查看试题解析
14. 钟表上的时间是3时20分，则此时时针与分针所成的夹角是度．

查看试题解析
15. 点C是线段AB上的三等分点，D是线段AC的中点，E是线段BC的中点，若CE＝6，则AB的长为．

查看试题解析

三、解答题

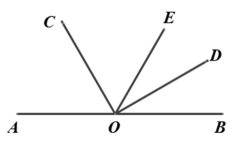
16. 计算：

(1)、16÷（﹣2）³+|﹣7|+（﹣ $\frac{1}{8}$ ）×（﹣4）；

(2)、5﹣（﹣0.25）﹣|﹣8|﹣ $\frac{1}{4}$ ．

查看试题解析
17. 解方程

(1)、3x－7(x－1)=3－2(x+3)

(2)、 $\frac{1 - x}{3} - x = 3 - \frac{x + 2}{4}$

查看试题解析
18. 已知 $a 、 b$ 互为相反数， $c 、 d$ 互为倒数， $x$ 是最大的负整数，求代数式的值： $x^{2} - (a + b + c d) x - {(a + b)}^{2} + {(- c d)}^{5}$ .

查看试题解析
19. 已知：如图，O是直线AB上的一点，∠COD＝90°，OC平分∠AOE，∠BOD＝30°，求∠DOE的度数．

查看试题解析
20. 在平面内有三点A，B，C，

(1)、当A，B，C三点不共线时，如图，画直线AC，线段BC，射线AB，在线段AB上任取一点D（不同于点A，B），连接CD，并数一数，此时图中共有多少条线段．

(2)、当A，B，C三点共线时，若AB=25cm，BC=16cm，点E、F分别是线段AB、BC的中点，求线段EF的长．（画出图形并写出计算过程）

查看试题解析
21. 小明解方程 $\frac{2 x - 1}{3} = \frac{x + a}{4} - 1$ ，去分母时方程右边的-1漏乘了12，因而求得方程的解为 $x = 3$ ，试求a的值，并符合题意求出方程的解.

查看试题解析
22. 某校开展校园艺术节系列活动，派小明到文体超市购买若干个文具袋作为奖品.这种文具袋标价每个10元，请认真阅读结账时老板与小明的对话图片，解决下面两个问题：

(1)、求小明原计划购买文具袋多少个？

(2)、学校决定，再次购买钢笔和签字笔共50支作为补充奖品，其中钢笔标价每支8元，签字笔标价每支6元.经过沟通，这次老板给予8折优惠，合计272元.问小明购买了钢笔和签字笔各多少支？

查看试题解析
23.

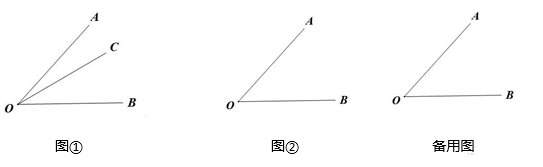(1)、（理解新知）

如图①，已知 $∠ A O B$ ，在 $∠ A O B$ 内部画射线 $O C$ ，得到三个角，分别为 $∠ A O C$ 、 $∠ B O C$ 、 $∠ A O B$ ，若这三个角中有一个角是另外一个角的2倍，则称射线 $O C$ 为 $∠ A O B$ 的“2倍角线”角的平分线这个角的“2倍角线”；（填“是”或“不是”）

(2)、若 $∠ A O B = 90 °$ ，射线 $O C$ 为 $∠ A O B$ 的“2倍角线”，则 $∠ A O C =$ $°$ ；

(3)、（解决问题）
如图②，已知 $∠ A O B = 60 °$ ，射线 $O P$ 从 $O A$ 出发，以每秒 $20 °$ 的速度绕O点逆时针旋转：射线 $O Q$ 从 $O B$ 出发，以每秒 $1 0^{∘}$ 的速度绕O点顺时针旋转，射线 $O P$ 、 $O Q$ 同时出发，当一条射线回到出发位置的时候，整个运动随之停止.设运动的时间为 $t (s)$ .

当射线 $O P$ 、 $O Q$ 旋转到同一条直线上时，求 $t$ 的值；

(4)、若 $O A$ 、 $O P$ 、 $O Q$ 三条射线中，一条射线恰好是以另外两条射线为边的角的“2倍角线”，直接写出所有可能的t的值.（本题中所研究的角都是小于等于 $18 0^{∘}$ 的角.）

查看试题解析