山东省济南市槐荫区2020-2021学年七年级上学期期末数学试题
试卷更新日期:2022-07-20 类型:期末考试
一、单选题
-
1. 在0,-2,5, , -0.3中,负数的个数是( ).A、1 B、2 C、3 D、42. 下列调查中,适宜采用全面调查方式的是( )A、了解一批圆珠笔的使用寿命 B、了解全国九年级学生身高的现状 C、考查人们保护海洋的意识 D、检查一枚用于发射卫星的运载火箭的各零部件3. 下列图形都是由完全相同的小正方形组成的,将它们分别沿虚线折叠后,不能围成一个小立方体的是( )A、
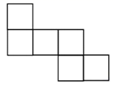 B、
B、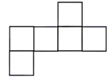 C、
C、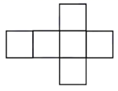 D、
D、 4. 为抗击新冠病毒疫情需要,总建筑面积约为79700平方米的雷神山医院迅速建成,耗时仅用10天,堪称“中国速度”的代表,更是“中国实力”的象征.数据79700用科学记数法表示应为( )A、 B、 C、 D、5. 下列运算中,正确的是( ).A、 B、 C、 D、6. 已知现有的8瓶可乐中有2瓶已过了保质期,从这8瓶可乐中随机抽取1瓶,恰好取到已过了保质期的可乐的概率是( )A、 B、 C、 D、7. 若代数式4x-5与 的值相等,则x的值是( )A、1 B、 C、 D、28. 下列说法正确的是( )A、最小的正整数是1 B、一个数的相反数一定比它本身小 C、绝对值等于它本身的数一定是正数 D、一个数的绝对值一定比0大9. 已知|a|=5,|b|=2,且a+b<0,则ab的值是( )A、10 B、﹣10 C、10或﹣10 D、﹣3或﹣710. 如图所示,两块三角板的直角顶点O重叠在一起,且恰好平分 , 则的度数是( )
4. 为抗击新冠病毒疫情需要,总建筑面积约为79700平方米的雷神山医院迅速建成,耗时仅用10天,堪称“中国速度”的代表,更是“中国实力”的象征.数据79700用科学记数法表示应为( )A、 B、 C、 D、5. 下列运算中,正确的是( ).A、 B、 C、 D、6. 已知现有的8瓶可乐中有2瓶已过了保质期,从这8瓶可乐中随机抽取1瓶,恰好取到已过了保质期的可乐的概率是( )A、 B、 C、 D、7. 若代数式4x-5与 的值相等,则x的值是( )A、1 B、 C、 D、28. 下列说法正确的是( )A、最小的正整数是1 B、一个数的相反数一定比它本身小 C、绝对值等于它本身的数一定是正数 D、一个数的绝对值一定比0大9. 已知|a|=5,|b|=2,且a+b<0,则ab的值是( )A、10 B、﹣10 C、10或﹣10 D、﹣3或﹣710. 如图所示,两块三角板的直角顶点O重叠在一起,且恰好平分 , 则的度数是( ) A、105° B、120° C、135° D、150°11. 已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,则线段MN的长度是( )
A、105° B、120° C、135° D、150°11. 已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,则线段MN的长度是( )
A、7cm B、3cm C、7cm或3cm D、5cm12. 一个纸环链,纸环按红黄绿蓝紫的顺序重复排列,被截去其中的一部分,剩下部分如图所示,则被截去部分纸环的个数可能是( ) A、2020 B、2019 C、2018 D、2017
A、2020 B、2019 C、2018 D、2017二、填空题
-
13. 的倒数是14. 若5与a-3互为相反数,则a的值为 .15. 小明家1至6月份的用水量统计如图所示,根据图中的数据可知,5月份的用水量比3月份的用水量多吨.
 16. 如果钟面上的时间是8:30,则分针与时针的夹角是度.17. 按照如图所示的程序计算,若 , 则输出的结果是 .
16. 如果钟面上的时间是8:30,则分针与时针的夹角是度.17. 按照如图所示的程序计算,若 , 则输出的结果是 . 18. 找规律: , , , , ……则第2020个数是 .
18. 找规律: , , , , ……则第2020个数是 .三、解答题
-
19. 计算:(1)、;(2)、 .20. 如图,已知直线l和直线外三点A,B,C,按下列要求画图:

⑴画射线AB;
⑵画直线CB;
⑶在直线l上确定点E,使得AE+CE最小.
21. 先化简,再求值: , 其中 .22. 解方程:(1)、;(2)、 .23. 为促进交于均能发展,A市实行“阳光分班”,某校七年级一班共有新生45人,其中男生比女生多3人,求该班男生、女生各有多少人.24. 每年夏天全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年某中学为确保学生安全,开展了“远离溺水,珍爱生命”的防溺水安全竞赛,学校对参加比赛的学生获奖情况进行了统计,绘制了如下两幅不完整的统计图,请结合图中相关数据解答下列问题. (1)、求参加此安全竞赛的学生共有多少人;(2)、在扇形统计图中,“三等奖”所对应的扇形的圆心角的度数为多少度?(3)、求获得二等奖的人数,并将条形统计图补充完整.25. 已知,O为直线上一点, .
(1)、求参加此安全竞赛的学生共有多少人;(2)、在扇形统计图中,“三等奖”所对应的扇形的圆心角的度数为多少度?(3)、求获得二等奖的人数,并将条形统计图补充完整.25. 已知,O为直线上一点, . (1)、如图,若 , 平分 .
(1)、如图,若 , 平分 .①求的度数;
②请通过计算说明是否平分 .
(2)、如图,若 , 求的度数. 26. 如图1是1个直角三角形和2个小正方形,直角三角形的三条边长分别是a、b、c,其中a、b是直角边,两个小正方形的边长分别是a、b.
26. 如图1是1个直角三角形和2个小正方形,直角三角形的三条边长分别是a、b、c,其中a、b是直角边,两个小正方形的边长分别是a、b. (1)、将4个完全一样的直角三角形和2个小正方形构成一个大正方形(如图2).用两种不同的方法列代数式表示图2中的大正方形面积:
(1)、将4个完全一样的直角三角形和2个小正方形构成一个大正方形(如图2).用两种不同的方法列代数式表示图2中的大正方形面积:方法一:;
方法二:;(直接把答案填写在答题卡的横线上)
(2)、观察图2,试写出 , , , 这四个代数式之间的等量关系: . (直接把答案填写在答题卡的横线上)(3)、请利用(2)中等量关系解决问题:若图1中一个三角形面积是6,图2的大正方形面积是64,求的值.27. 已知线段个单位长度. (1)、如图1,点P沿线段自点A出发向点B以1个单位长度每秒的速度运动,同时点Q沿线段自点B出发向点A以2个单位长度每秒的速度运动,几秒钟后,P、Q两点相遇?(2)、如图1,几秒后,P、Q两点相距3个单位长度?
(1)、如图1,点P沿线段自点A出发向点B以1个单位长度每秒的速度运动,同时点Q沿线段自点B出发向点A以2个单位长度每秒的速度运动,几秒钟后,P、Q两点相遇?(2)、如图1,几秒后,P、Q两点相距3个单位长度? (3)、如图2,个单位长度, 个单位长度,当点P在的上方,且时,点P绕着点O以30度/秒的速度在圆周上逆时针旋转一周停止,同时点Q沿线段自B点向A点运动,假若P、Q两点能相遇,求点Q的运动速度.
(3)、如图2,个单位长度, 个单位长度,当点P在的上方,且时,点P绕着点O以30度/秒的速度在圆周上逆时针旋转一周停止,同时点Q沿线段自B点向A点运动,假若P、Q两点能相遇,求点Q的运动速度.