山东省菏泽市鄄城县2020-2021学年七年级上学期期末数学试题
试卷更新日期:2022-07-20 类型:期末考试
一、单选题
-
1. 在下列调查中,适宜采用全面调查的是( )A、了解我省中学生的视力情况 B、了解七(1)班学生校服的尺码情况 C、检测一批电灯泡的使用寿命 D、调查安徽卫视《超级演说家》栏目的收视率2. 新亚欧大陆桥东起太平洋西岸中国连云港,西达大西洋东岸荷兰鹿特丹等港口,横贯亚欧两大洲中部地带,总长约为10900公里,10900用科学记数法表示为( )A、0.109×105 B、1.09×104 C、1.09×103 D、109×1023. 有下列说法:①由许多条线段连接而成的图形叫做多边形;②从一个多边形(边数为n)的同一个顶点出发,分别连接这个顶点与其余与之不相邻的各顶点,可以把这个多边形分割成个三角形;③角的边越长,角越大;④一条射线就是一个周角.其中正确的结论有( )A、1个 B、2个 C、3个 D、0个4. 下列说法中错误的是( )A、- x2y的系数是- B、0是单项式 C、 xy的次数是1 D、-x是一次单项式5. 一个物体的外形是圆柱,但不清楚它的内部结构,现用一组水平的平面去截这个物体,从上至下的五个截面依次如图所示,则这个物体可能是下列选项中的( ).
 A、
A、 B、
B、 C、
C、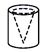 D、
D、 6. 若是方程的解,则关于y的方程的解是( )A、 B、 C、 D、7. 如图所示的两台天平保持平衡,已知每块巧克力的重量相等,且每个果冻的重量也相等,则每块巧克力和每个果冻的重量分别为( )
6. 若是方程的解,则关于y的方程的解是( )A、 B、 C、 D、7. 如图所示的两台天平保持平衡,已知每块巧克力的重量相等,且每个果冻的重量也相等,则每块巧克力和每个果冻的重量分别为( )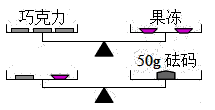 A、 , B、 , C、 , D、 ,8. 如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=20°,则∠AOB等于( ).
A、 , B、 , C、 , D、 ,8. 如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=20°,则∠AOB等于( ). A、50° B、40° C、30° D、20°
A、50° B、40° C、30° D、20°二、填空题
-
9. 三棱锥有个顶点,个面,条棱.10. -的相反数是 , 绝对值是 , 倒数是.11. 某校为丰富校园文化生活,打算从“文化演出”“运动会”“演讲比赛”三项活动中选出一项,为此调查了本校所有学生,调查的结果如图所示,根据图中给出的信息,这所学校赞成举办演讲比赛的学生有人.
 12. 上午9点30分,时钟的时针和分针成的角为 .13. 一家体育器材商店,将某种品牌的篮球按成本价提高40%后标价,又以8折(即按标价的80%)优惠卖出.已知每个篮球的成本价为a元,则该商店卖出一个篮球可获利润元.14. 已知 , , 则的值为 .
12. 上午9点30分,时钟的时针和分针成的角为 .13. 一家体育器材商店,将某种品牌的篮球按成本价提高40%后标价,又以8折(即按标价的80%)优惠卖出.已知每个篮球的成本价为a元,则该商店卖出一个篮球可获利润元.14. 已知 , , 则的值为 .三、解答题
-
15. 计算:(1)、;(2)、 .16. 解下列方程:(1)、;(2)、 .17. 如图是由几个大小完全一样的小正方体搭成的几何体从上面看得到的图形,小正方形中的数字表示在该位置小正方体的个数,请你分别画出从正面看和从左面看该几何体得到的图形.
 18. 先化简,再求值:2x-[2(x+4)-3(x+2y)]-2y,其中 .19. 某校计划组织学生到市影剧院观看大型感恩歌舞剧,为了解学生如何去影剧院的问题,学校随机抽取部分学生进行调查,并将调查结果制成了表格、条形统计图和扇形统计图(均不完整).
18. 先化简,再求值:2x-[2(x+4)-3(x+2y)]-2y,其中 .19. 某校计划组织学生到市影剧院观看大型感恩歌舞剧,为了解学生如何去影剧院的问题,学校随机抽取部分学生进行调查,并将调查结果制成了表格、条形统计图和扇形统计图(均不完整). (1)、此次共调查了多少位学生?(2)、将表格填充完整;
(1)、此次共调查了多少位学生?(2)、将表格填充完整;步行
骑自行车
坐公共汽车
其他
50
(3)、将条形统计图补充完整.20. 如图, , , E、F分别是、的中点,求的长. 21. 周末,小明和爸爸在400米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:
21. 周末,小明和爸爸在400米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:
请根据他们的对话内容,求小明和爸爸的骑行速度.
22. 已知ab>0,a+b<0,|a|=5,|b|=2,求a3+b2-ab的值.23. 如图,已知∠BAE=∠CAF=110°,∠CAE=60°,AD是∠BAF的角平分线,求∠BAD的度数. 24. 阅读理解:若A、B、C为数轴上三点,点C是线段上一点,若点C到点A的距离是点C到点B的距离的2倍,我们就称点C是(A,B)的好点,如图1,点A表示的数为-1,点B表示的数为2,表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;又如,表示0的点D到点A的距离是1,到点B距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.
24. 阅读理解:若A、B、C为数轴上三点,点C是线段上一点,若点C到点A的距离是点C到点B的距离的2倍,我们就称点C是(A,B)的好点,如图1,点A表示的数为-1,点B表示的数为2,表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;又如,表示0的点D到点A的距离是1,到点B距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.
知识运用:如图2,M、N为数轴上两点,点M所表示的数为 , 点N所表示的数为4. (1)、数所表示的点是(M,N)的好点;(2)、如图3,A、B为数轴上两点,点A所表示的数为-20,点B所表示的数为40,现有一只电子蚂蚁P从点B出发,以每秒2个单位的速度向左运动,到达点A时停止,运动的时间为t秒.当t为何值时,点P、A和B中恰有一个点为其余两点的好点?
(1)、数所表示的点是(M,N)的好点;(2)、如图3,A、B为数轴上两点,点A所表示的数为-20,点B所表示的数为40,现有一只电子蚂蚁P从点B出发,以每秒2个单位的速度向左运动,到达点A时停止,运动的时间为t秒.当t为何值时,点P、A和B中恰有一个点为其余两点的好点?