山东省菏泽市成武县2020-2021学年七年级上学期期末数学试题
试卷更新日期:2022-07-20 类型:期末考试
一、单选题
-
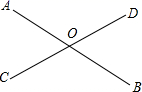
1. 下列算式中,计算结果是负数的是A、 B、 C、 D、2. 下列说法:① 一定是负数;② 一定是正数;③倒数等于它本身的数是 ;④绝对值等于它本身的数是l;⑤平方等于它本身的数是1.其中正确的个数是( )A、1个 B、2个 C、3个 D、4个3. 如图,直线AB、CD相交于点O,在这两条直线上,与点O的距离为3cm的点有( )
 A、2个 B、3个 C、4个 D、5个4. 中学生骑电动车上学给交通安全带来隐患,为了解中学2 000名学生家长对“中学生骑电动车上学”的态度,从中随机调查400名家长,结果有360名家长持反对态度,则下列说法正确的是( )A、调查方式是普查 B、该校只有360名家长持反对态度 C、样本是360名家长 D、该校约有90%的家长持反对态度5. 如果a与b互为相反数且x与y互为倒数,那么 的值为( )A、0 B、-2 C、-1 D、无法确定6. 一种商品进价为每件a元,按进价增加出售,则增加后的售价为每件( )元.A、 B、 C、 D、7. 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳记数”.一位书生坚持每天五更起床读书,为了勉励自己,他用“结绳记数”的方法来记录自己读书的天数,如图1是他从右到左依次排列的绳子上打结,满六进一,表示的天数为天(),按同样的方法,图2表示的天数是( )
A、2个 B、3个 C、4个 D、5个4. 中学生骑电动车上学给交通安全带来隐患,为了解中学2 000名学生家长对“中学生骑电动车上学”的态度,从中随机调查400名家长,结果有360名家长持反对态度,则下列说法正确的是( )A、调查方式是普查 B、该校只有360名家长持反对态度 C、样本是360名家长 D、该校约有90%的家长持反对态度5. 如果a与b互为相反数且x与y互为倒数,那么 的值为( )A、0 B、-2 C、-1 D、无法确定6. 一种商品进价为每件a元,按进价增加出售,则增加后的售价为每件( )元.A、 B、 C、 D、7. 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳记数”.一位书生坚持每天五更起床读书,为了勉励自己,他用“结绳记数”的方法来记录自己读书的天数,如图1是他从右到左依次排列的绳子上打结,满六进一,表示的天数为天(),按同样的方法,图2表示的天数是( )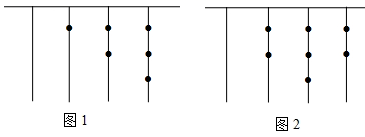 A、 B、 C、 D、8. 对于单项式x,下列说法中正确的是( )A、系数是0,次数是0 B、系数是1,次数是0 C、系数是0,次数是1 D、系数是1,次数是19. 下列等式恒成立的是( )A、 B、 C、 D、10. 下列一元一次方程中,解为x=3的是( )A、x+3=0 B、5x+7=7﹣2x C、2x﹣4=4x﹣2 D、3x﹣2=4+x
A、 B、 C、 D、8. 对于单项式x,下列说法中正确的是( )A、系数是0,次数是0 B、系数是1,次数是0 C、系数是0,次数是1 D、系数是1,次数是19. 下列等式恒成立的是( )A、 B、 C、 D、10. 下列一元一次方程中,解为x=3的是( )A、x+3=0 B、5x+7=7﹣2x C、2x﹣4=4x﹣2 D、3x﹣2=4+x二、填空题
-
11. 如图,直角三角形绕直线L旋转一周,得到的立体图形是.
 12. 如果一个数的相反数等于它本身,那么这个数是 .13. 函数 , 则当自变量时, .14. 某班生活委员将全班同学的年龄情况绘制成了如图所示的条形统计图,则全班共有 名学生.
12. 如果一个数的相反数等于它本身,那么这个数是 .13. 函数 , 则当自变量时, .14. 某班生活委员将全班同学的年龄情况绘制成了如图所示的条形统计图,则全班共有 名学生.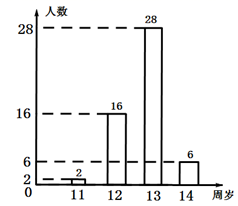 15. 多项式 与 相加后不含 的二次项,则常数 的值等于 .16. 已知方程 是关于 的一元一次方程,则 的值是 .
15. 多项式 与 相加后不含 的二次项,则常数 的值等于 .16. 已知方程 是关于 的一元一次方程,则 的值是 .三、解答题
-
17. 化简:(1)、;(2)、;18. 用直尺和圆规作图,不写作法,但要保留作图痕迹.
如图,已知线段a、b,求作:线段 , 使 .
 19. 某中学为了解该校学生的课余活动情况,采用抽样调查的方式,从运动、娱乐、阅读和其他四个方面调查了若干名学生的兴趣和爱好情况,并根据调查结果制作了如下两幅统计图.
19. 某中学为了解该校学生的课余活动情况,采用抽样调查的方式,从运动、娱乐、阅读和其他四个方面调查了若干名学生的兴趣和爱好情况,并根据调查结果制作了如下两幅统计图.
根据图中提供的信息解答下列问题:
(1)、求本次抽样调查的人数;(要求列式计算,写出求解过程)(2)、补全人数统计图;(3)、“运动”对应的扇形的圆心角度数是 ▲ 度.20. 解方程:(1)、 .(2)、 .21. 高斯上小学时,有一次数学老师让同学们计算“从到这个正整数的和",许多同学都采用了依次累加的计算方法,计算起来非常烦琐,并且容易出错,聪明的小高斯经过探索后,给出了下面漂亮的解答过程:解:设 , ①
则 , ②
①②,得
.
, ③
.
后来人们将小高斯的这种解答方法概括为“倒序相加法”
(1)、请你运用高斯的“倒序相加法”计算:;(2)、请你认真观察上面解答过程中的③式及你运算过程中出现类似的③式,猜想 ▲ (用含n的代数式表示);(3)、计算: .22. 已知 .(1)、如果 , 求y的值;(2)、求的值.