山东省德州市禹城市2020-2021学年七年级上学期期末数学试题

试卷更新日期：2022-07-20 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各组数中，相等的是（）

A、 $- (- 2)^{2}$ 和 $- (- 2^{2})$ B、 $- (- 2)^{2}$ 和 $- (+ 2)^{2}$ C、 $- (- 2)$ 和 $- | - 2 |$ D、 $- (- 2)$ 和 $- (+ 2)$

查看试题解析
2. 某市区人口总数大约540万，这个数用科学记数法应该表示为（）

A、 $54 \times 1 0^{5}$ B、 $0.54 \times 1 0^{7}$ C、 $5.4 \times 1 0^{6}$ D、 $5.4 \times 1 0^{7}$

查看试题解析
3. 已知有理数a、b在数轴上对应的点如图所示，则下列式子正确的是（）

A、a•b＞0 B、a+b＜0 C、|a|＜|b| D、a﹣b＞0

查看试题解析
4. 在下列生活、生产现象中，不可以用基本事实“两点确定一条直线”来解释的有（）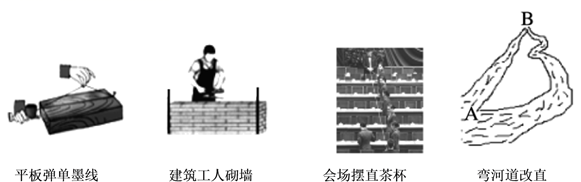

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 下列说法中正确的是（）

A、3 $x^{2}$ 、－ $\frac{1}{7}$ xy、0、m四个式子中有三个是单项式 B、单项式2πxy的系数是2 C、式子 $\frac{3}{x} + 7 x^{2} y$ 是三次二项式 D、－ $\frac{1}{5} x^{2} y^{3}$ 和6 $y^{3} x^{2}$ 是同类项

查看试题解析
6. 下列变形后的等式不一定成立的是（）

A、若 $x = y$ ，则 $x + 5 = y + 5$ B、若 $\frac{x}{a} = \frac{y}{a}$ ，则 $x = y$ C、若 $x = y$ ，则 $x^{2} = y^{2}$ D、若 $m x = m y$ ，则 $x = y$

查看试题解析
7. 一商店在某一时间以每件 $a$ 元的价格卖出两件衣服，其中一件盈利25%，另一件亏损25%，卖这两件衣服总共亏损4元，则 $a$ 的值为（）

A、30 B、40 C、50 D、60

查看试题解析
8. 多项式 $3 x^{| m |} y^{2} + (m + 2) x^{2} y - 1$ 是关于x、y的四次三项式，则m的值为（）

A、±2 B、-2 C、2 D、±1

查看试题解析
9. 图中所示几何体从上面看，得到的平面图形为（）

A、 B、 C、 D、

查看试题解析
10. 一项工程，甲单独做5天完成，乙单独做8天完成.若甲先做1天,然后甲、乙合作完成此项工作的 $\frac{3}{4}$ .若设甲一共做了x天，则所列方程为（）

A、 $\frac{x}{5} + \frac{x + 1}{8} = \frac{3}{4}$ B、 $\frac{x}{5} + \frac{x - 1}{8} = \frac{3}{4}$ C、 $\frac{x}{5} - \frac{x + 1}{8} = \frac{3}{4}$ D、 $\frac{x}{5} - \frac{x - 1}{8} = \frac{3}{4}$

查看试题解析
11. 有理数a，b，c在数轴上的位置如图所示：则代数式 $| a + c | - 2 | a - b | + | b - c |$ ，化简后的结果为（）

A、 $a + b$ B、 $a + 2 b$ C、 $a - 3 b$ D、 $a - 2 b$

查看试题解析
12. 小明家的窗户上有一些精致花纹，小明对此非常感兴趣，他观察发现窗格的花纹排列呈现有一定规律，如图，其中“○”代表的就是精致的花纹，请问有47个精致花纹的是第（）个图

A、11 B、13 C、15 D、17

查看试题解析

二、填空题

13. 已知 $| a | = 5$ ， $| b | = 2$ ，且 $a + b < 0$ ，则 $a b$ 的值是.

查看试题解析
14. 若角 $α$ 的补角等于它的余角的6倍，则角 $α$ 等于.

查看试题解析
15. 如图所示，将一平行四边形纸片ABCD沿AE，EF折叠，使点E，B₁ ， C₁在同一条直线上，则∠AEF=.

查看试题解析
16. 若x＝2y+3，则代数式3x﹣6y+1的值是．

查看试题解析
17. 小王从家出发向南偏东30°的方向走了100米到达小军家，此时小王家在小军家的方向．

查看试题解析
18. 规定⊗是一种新运算规则：a⊗b＝a²﹣b² ，例如：2⊗3＝2²﹣3²＝4﹣9＝﹣5，则5⊗[1⊗（﹣2）]＝.

查看试题解析

三、解答题

19. 计算

(1)、 $(- 2)^{2} - | - 8 | + 3 - 2 \times (- \frac{1}{2})$

(2)、 $(- \frac{1}{2} + \frac{2}{3} - \frac{1}{4}) \times | - 24 |$

查看试题解析
20. 解下列方程：

(1)、 $3 (7 - x) = 18 - 2 (3 x - 15)$

(2)、 $\frac{2 x + 4}{4} - \frac{3 x - 2}{2} = 1$

查看试题解析
21. 先化简再求值： $(a b + 3 a^{2}) - 2 b^{2} - 5 a b - 2 (a^{2} - 2 a b)$ ，其中 $| a - 1 | + (b + 2)^{2} = 0$ ．

查看试题解析
22.

(1)、已知x=﹣3是关于x的方程2k﹣x﹣k（x+4）=5的解，求k的值；

(2)、在（1）的条件下，已知线段AB=12cm，点C是直线AB上一点，且BC=k•AC，若点D是AC的中点，求线段CD的长.

查看试题解析
23. 我们称使方程 $\frac{x}{2} + \frac{y}{3} = \frac{x + y}{2 + 3}$ 成立的一对数 $x ， y$ 为“相伴数对”，记为 $(x ， y)$ .

(1)、若 $(4 ， y)$ 是“相伴数对”，求 $y$ 的值：

(2)、若 $(a ， b)$ 是“相伴数对”，请用含 $b$ 的代数式表示 $a$ ；

(3)、若 $(m ， n)$ 是“相伴数对”，求代数式 $m - \frac{22}{3} n - [4 m - 2 (3 n - 1)]$ 的值

查看试题解析
24. 如图，已知∠AOB为直角，∠AOC为锐角，且OM平分∠BOC，ON平分∠AOC．

(1)、如果∠AOC=50°，求∠MON的度数．

(2)、如果∠AOC为任意一个锐角，你能求出∠MON的度数吗？若能，请求出来，若不能，说明为什么？

查看试题解析
25. 在天府新区的建设中，现要把176吨物资从某地运往华阳的甲、乙两地，用大、小两种货车共18辆，恰好能一次性运完这批物资．已知这两种货车的载重量分别为12吨/辆和8吨/辆，运往甲、乙两地的运费如下表：

运往地

车型

甲地（元/辆）

乙地（元/辆）

大货车

640

680

小货车

500

560

(1)、求这两种货车各用多少辆？

(2)、如果安排10辆货车前往甲地，其余货车前往乙地，设前往甲地的大货车为a辆，运往甲、乙两地的总运费为w元，求出w与a的关系式；

(3)、在（2）的条件下，若运往甲地的物资为100吨，请求出安排前往甲地的大货车多少辆，并求出总运费．

查看试题解析