山东省德州市夏津县2020-2021学年七年级上学期期末数学试题
试卷更新日期:2022-07-20 类型:期末考试
一、单选题
-
1. 2020年1月12日,夏津县白天的最高气温 , 夜间气温最低时 , 则这天的温差为( )A、 B、 C、 D、2. 用四舍五入法按要求把2.0503分别取近似数,其中错误的是( )A、2.1(精确到0.1) B、2.05(精确到0.001) C、2.05(精确到百分位) D、2.050(精确到千分位)3. 下列变形正确的是( )A、由得 B、由得 C、由 , 得 D、由得4. 单项式﹣的系数、次数分别是( )A、﹣1,2 B、﹣1,4 C、﹣ , 2 D、﹣ , 45. 一项工程,甲单独做5天完成,乙单独做8天完成.若甲先做1天,然后甲、乙合作完成此项工作的 .若设甲一共做了x天,则所列方程为( )A、 B、 C、 D、6. 下列图形中,线段AD的长表示点A到直线BC距离的是( )
A、 B、
B、 C、
C、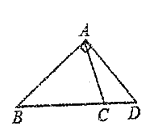 D、
D、 7. 如图,直线 AD,BE 被直线 BF 和 AC所截,则∠1的同位角和∠5的内错角分别是( )
7. 如图,直线 AD,BE 被直线 BF 和 AC所截,则∠1的同位角和∠5的内错角分别是( ) A、∠4,∠2 B、∠2,∠6 C、∠5,∠4 D、∠2,∠48. 如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能符合题意解释这一现象的数学知识是( )
A、∠4,∠2 B、∠2,∠6 C、∠5,∠4 D、∠2,∠48. 如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能符合题意解释这一现象的数学知识是( )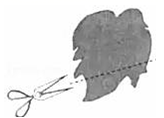 A、垂线段最短 B、经过一点有无数条直线 C、两点之间,线段最短 D、经过两点,有且仅有一条直线9. 下列命题中,是真命题的是( )A、在同一平面内,垂直于同一直线的两条直线平行 B、相等的角是对顶角 C、两条直线被第三条直线所截,同旁内角互补 D、过一点有且只有一条直线与已知直线平行10. 某种衬衫因换季打折出售,如果按原价的六折出售,那么每件赔本40元;按原价的九折出售,那么每件盈利20元,则这种衬衫的原价是( )A、160元 B、180元 C、200元 D、220元11. 如图所示,下列判断错误的是( )
A、垂线段最短 B、经过一点有无数条直线 C、两点之间,线段最短 D、经过两点,有且仅有一条直线9. 下列命题中,是真命题的是( )A、在同一平面内,垂直于同一直线的两条直线平行 B、相等的角是对顶角 C、两条直线被第三条直线所截,同旁内角互补 D、过一点有且只有一条直线与已知直线平行10. 某种衬衫因换季打折出售,如果按原价的六折出售,那么每件赔本40元;按原价的九折出售,那么每件盈利20元,则这种衬衫的原价是( )A、160元 B、180元 C、200元 D、220元11. 如图所示,下列判断错误的是( ) A、若∠1=∠3,AD∥BC,则BD是∠ABC的平分线 B、若AD∥BC,则∠1=∠2=∠3 C、若∠3+∠4+∠C=180°,则AD∥BC D、若∠2=∠3,则AD∥BC12. 若代数式(为常数)的值与字母x的取值无关,则代数式的值为( )A、 B、 C、或 D、13. 对于式子 , 下列说法正确的是( )A、有5个单项式,1个多项式 B、有3个单项式,2个多项式 C、有4个单项式,2个多项式 D、有7个整式14. 下列说法:①整数是正整数和负整数的统称;②一定是正数;③倒数等于它本身的数是;④绝对值等于它本身的数是;⑤平方等于它本身的数是 , 其中正确的个数是( )A、个 B、个 C、个 D、个15. 若x=2是关于x的一元一次方程ax-2=b的解,则3b-6a+2的值是( ).A、-8 B、-4 C、8 D、416. 用棋子摆出下列一组图形:
A、若∠1=∠3,AD∥BC,则BD是∠ABC的平分线 B、若AD∥BC,则∠1=∠2=∠3 C、若∠3+∠4+∠C=180°,则AD∥BC D、若∠2=∠3,则AD∥BC12. 若代数式(为常数)的值与字母x的取值无关,则代数式的值为( )A、 B、 C、或 D、13. 对于式子 , 下列说法正确的是( )A、有5个单项式,1个多项式 B、有3个单项式,2个多项式 C、有4个单项式,2个多项式 D、有7个整式14. 下列说法:①整数是正整数和负整数的统称;②一定是正数;③倒数等于它本身的数是;④绝对值等于它本身的数是;⑤平方等于它本身的数是 , 其中正确的个数是( )A、个 B、个 C、个 D、个15. 若x=2是关于x的一元一次方程ax-2=b的解,则3b-6a+2的值是( ).A、-8 B、-4 C、8 D、416. 用棋子摆出下列一组图形:
按照这种规律摆下去,第个图形用的棋子个数为( )
A、 B、 C、 D、二、填空题
-
17. 如果a、b互为倒数,c、d互为相反数,且 ,则 .18. 将一张长方形纸折叠成如图所示的形状,则 的度数是 .
 19. 数轴上表示-4.5与2.5之间的所有整数之和是 .20. 一个角的补角比它的余角的3倍还多10°,则这个角的度数为 .21. 某儿童服装店老板以元的价格买进件连衣裙,针对不同的顾客,30件连衣裙的售价不完全相同,若以45元为标准,将超过的钱数记为正,不足的钱数记为负,记录结果如下表:
19. 数轴上表示-4.5与2.5之间的所有整数之和是 .20. 一个角的补角比它的余角的3倍还多10°,则这个角的度数为 .21. 某儿童服装店老板以元的价格买进件连衣裙,针对不同的顾客,30件连衣裙的售价不完全相同,若以45元为标准,将超过的钱数记为正,不足的钱数记为负,记录结果如下表:售出件数
7
6
3
5
4
5
售价(元)
该服装店售完这30件连衣裙后,赚了元.
22. 如图,将一副三角板摆放到两条平行线间,两个三角板的直角边共线,含30°角的三角板的斜边与一条平行线共线,含45°角的三角板的一个顶点在另一条平行线上则,∠1= .
三、解答题
-
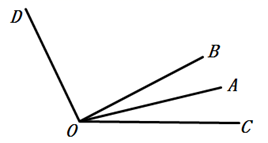
23. 计算:(1)、(2)、24. 解下列方程:(1)、(2)、25. 如图∠COD=116°,∠BOD=90°,OA平分∠BOC,求∠AOD的度数.
 26. 已知(1)、化简:;(2)、已知与是同类项,求的值.27. 如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF⊥CD于E.
26. 已知(1)、化简:;(2)、已知与是同类项,求的值.27. 如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF⊥CD于E. (1)、求证:AD∥BC;(2)、若∠ADB=36°,求∠EFC的度数.28. 已知是关于x的方程的解.(1)、求k的值;(2)、在(1)的条件下,已知线段 , 点C是直线上一点,且 , 若点D是的中点,求线段的长.(注意:先画出对应的图形再求解)29. 对于任意四个有理数 , 可以组成两个有理数对与 . 我们规定: . 例如: . 根据上述规定解决下列问题:(1)、求;(2)、若 , 求;(3)、当满足等式的是整数时,求整数k的值.30. 为发展校园足球运动,某城区四校决定联合购买一批足球运动装备.市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球服和足球,已知每套队服比每个足球多元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过套,则购买足球打八折.(1)、求每套队服和每个足球的价格是多少元;(2)、若城区四校联合购买套队服和个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花费用;(3)、在(2)的条件下,计算a为何值时,两家商场所花费用相同;(4)、在(3)的条件下,假如你是本次购买任务的负责人,你认为到甲、乙哪家商场购买比较合算?(直接写出方案)
(1)、求证:AD∥BC;(2)、若∠ADB=36°,求∠EFC的度数.28. 已知是关于x的方程的解.(1)、求k的值;(2)、在(1)的条件下,已知线段 , 点C是直线上一点,且 , 若点D是的中点,求线段的长.(注意:先画出对应的图形再求解)29. 对于任意四个有理数 , 可以组成两个有理数对与 . 我们规定: . 例如: . 根据上述规定解决下列问题:(1)、求;(2)、若 , 求;(3)、当满足等式的是整数时,求整数k的值.30. 为发展校园足球运动,某城区四校决定联合购买一批足球运动装备.市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球服和足球,已知每套队服比每个足球多元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过套,则购买足球打八折.(1)、求每套队服和每个足球的价格是多少元;(2)、若城区四校联合购买套队服和个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花费用;(3)、在(2)的条件下,计算a为何值时,两家商场所花费用相同;(4)、在(3)的条件下,假如你是本次购买任务的负责人,你认为到甲、乙哪家商场购买比较合算?(直接写出方案)