山东省滨州市惠民县2020-2021学年七年级上学期期末数学试题
试卷更新日期:2022-07-20 类型:期末考试
一、单选题
-
1. 在实数 , , 0,1中最大的数是( ).A、 B、 C、0 D、12. 习近平总书记提出精准扶贫战略以来,各地积极加大帮扶力度,全国脱贫人口数不断增加,脱贫人口接近189000000人,数据189000000可用科学记数法表示为( ).A、 B、 C、 D、3. 如图,直线a、b被直线c所截, ,若 ,则 的度数为( )
 A、 B、 C、 D、4. 下列结论正确的是( ).A、和是同类项 B、不是单项式 C、a比大 D、是六次单项式5. 下列说法错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则6. 下列命题正确的是( ).A、内错角相等 B、一个角的度数为 , 则这个角的余角和补角的度数分别为 , C、甲看乙的方向为北偏东 , 那么乙看甲的方向南偏西 D、在同一平面内,a,b,c是直线,且 , , 则7. 如图,一副三角尺按不同的位置摆放,摆放位置中 的图形的个数是( )
A、 B、 C、 D、4. 下列结论正确的是( ).A、和是同类项 B、不是单项式 C、a比大 D、是六次单项式5. 下列说法错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则6. 下列命题正确的是( ).A、内错角相等 B、一个角的度数为 , 则这个角的余角和补角的度数分别为 , C、甲看乙的方向为北偏东 , 那么乙看甲的方向南偏西 D、在同一平面内,a,b,c是直线,且 , , 则7. 如图,一副三角尺按不同的位置摆放,摆放位置中 的图形的个数是( )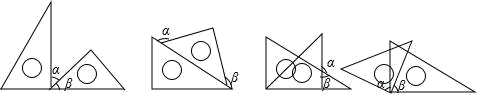 A、 B、 C、 D、8. 如果是关于x的方程的解,则的值是( ).A、-2 B、2 C、-1 D、19. 点M,N,P和原点O在数轴上的位置如图所示,点M,N,P表示的有理数为a,b,c(对应顺序暂不确定).如果bc<0,b+c>0,ab>ac,那么表示数c的点为( )
A、 B、 C、 D、8. 如果是关于x的方程的解,则的值是( ).A、-2 B、2 C、-1 D、19. 点M,N,P和原点O在数轴上的位置如图所示,点M,N,P表示的有理数为a,b,c(对应顺序暂不确定).如果bc<0,b+c>0,ab>ac,那么表示数c的点为( ) A、点M B、点N C、点P D、点O10. 观察下列各式:31=3,32=9,33=27,34=81,35=243,36=729,…则:32018的个位数字是( )A、3 B、9 C、7 D、111. 如图,某同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长小,能符合题意解释这一现象的数学知识是:( )
A、点M B、点N C、点P D、点O10. 观察下列各式:31=3,32=9,33=27,34=81,35=243,36=729,…则:32018的个位数字是( )A、3 B、9 C、7 D、111. 如图,某同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长小,能符合题意解释这一现象的数学知识是:( )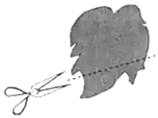 A、两点之间,直段最短 B、两点确定一条直线 C、两点之间,线段最短 D、经过一点有无数条直线12. 如图,是一个正方体盒子的展开图,则这个正方体可能是( ).
A、两点之间,直段最短 B、两点确定一条直线 C、两点之间,线段最短 D、经过一点有无数条直线12. 如图,是一个正方体盒子的展开图,则这个正方体可能是( ). A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
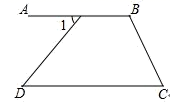
13. 比较大小:-5-6(填“>”,“<”或“=”).14. 如图,AB∥CD,∠1=48°,∠C和∠D互余,则∠B=°.
 15. 如图,在长方形ABCD中,线段AC,BD相交于O,DE//AC,CE//BD,BC=2cm,那么三角形EDC可以看作由平移得到的,连接OE,则OE=cm.
15. 如图,在长方形ABCD中,线段AC,BD相交于O,DE//AC,CE//BD,BC=2cm,那么三角形EDC可以看作由平移得到的,连接OE,则OE=cm. 16. 某工程,甲单独做需要12天完成,乙单独做需要8天完成,现由甲先做3天,乙再与甲合作完成这项工程,求完成这项工程时甲总共用的时间.若设完成这项工程时甲共用了 天,则依题意可列方程 .17. 如图,射线 , 把 三等分,若图中所有小于平角的角的度数之和是 ,则 的度数为 .
16. 某工程,甲单独做需要12天完成,乙单独做需要8天完成,现由甲先做3天,乙再与甲合作完成这项工程,求完成这项工程时甲总共用的时间.若设完成这项工程时甲共用了 天,则依题意可列方程 .17. 如图,射线 , 把 三等分,若图中所有小于平角的角的度数之和是 ,则 的度数为 .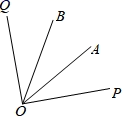 18. 一个书包的标价为115元,按8折出售仍可获利15%,该书包的进价为元.19. 一般情况下不成立,但有些数可以使得它成立,例如 . 我们称使得成立的一对数m,n为“相伴数对”,记为 . 若是“相伴数对”,则 .20. 如图,用大小相同的小正方形拼大正方形,拼第1个大正方形需要4个小正方形,拼第2个大正方形需要9个小正方形,拼第3个大正方形需要16个小正方形,……,按照这样的拼法,第9个大正方形比第8个大正方形多个小正方形.
18. 一个书包的标价为115元,按8折出售仍可获利15%,该书包的进价为元.19. 一般情况下不成立,但有些数可以使得它成立,例如 . 我们称使得成立的一对数m,n为“相伴数对”,记为 . 若是“相伴数对”,则 .20. 如图,用大小相同的小正方形拼大正方形,拼第1个大正方形需要4个小正方形,拼第2个大正方形需要9个小正方形,拼第3个大正方形需要16个小正方形,……,按照这样的拼法,第9个大正方形比第8个大正方形多个小正方形.
三、解答题
-
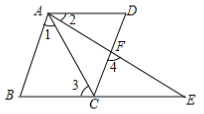
21. 先化简,再求值∶(1)、 , 其中x=2,y=3.(2)、 , 其中a=-2,b=1.22.(1)、计算∶;(2)、计算∶;(3)、解方程∶;(4)、解方程∶ .23. 如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4,求证:AD∥BE.
 24. 如图,O是直线AB上一点,∠AOE=∠COD,射线OC平分∠BOE,∠EOC=50°.求∠DOE的度数.
24. 如图,O是直线AB上一点,∠AOE=∠COD,射线OC平分∠BOE,∠EOC=50°.求∠DOE的度数. 25. 已知线段 , 点在线段上,F是线段的中点(1)、如图1,当E是线段的中点时,求线段的长;
25. 已知线段 , 点在线段上,F是线段的中点(1)、如图1,当E是线段的中点时,求线段的长; (2)、如图2.当E是线段的中点时,请你写出线段与线段之间的数量关系.
(2)、如图2.当E是线段的中点时,请你写出线段与线段之间的数量关系. 26. “迎新年”信誉楼开展促销活动,出售A、B两种商品,活动方式有如下两种:
26. “迎新年”信誉楼开展促销活动,出售A、B两种商品,活动方式有如下两种:商品
A
B
单价(单位:元)
80
120
方式一
折数
六折
八折
方式二
若购买达到或超过100件(A、B两种商品可累计),则打七折优惠
(同一种商品不可同时参与两种活动)
(1)、某单位购买A商品50件,B商品60件,选择何种活动方式更划算?能便宜多少钱?(2)、某单位购买A、B两种商品共100件,当购买A商品x件(x为正整数)时,该单位选择何种活动方式更划算?请说明理由.27. 已知∶点A、C、B不在同一条直线上,AD∥BE. (1)、如图①,当∠A=58°,∠B=118°时,求∠C的度数;(2)、如图②,AQ、BQ分别为∠DAC、∠EBC的平分线所在直线,试探究∠C与∠AQB的数量关系;(3)、如图③,在(2)的前提下,且有AC∥OB,QP⊥PB,直接写出∠DAC∶∠ACB∶∠CBE的值.
(1)、如图①,当∠A=58°,∠B=118°时,求∠C的度数;(2)、如图②,AQ、BQ分别为∠DAC、∠EBC的平分线所在直线,试探究∠C与∠AQB的数量关系;(3)、如图③,在(2)的前提下,且有AC∥OB,QP⊥PB,直接写出∠DAC∶∠ACB∶∠CBE的值.