山东省滨州市滨城区2020-2021学年七年级上学期期末数学试题
试卷更新日期:2022-07-20 类型:期末考试
一、单选题
-
1. 如果水位升高0.6 m时水位变化记作 , 那么水位下降0.4m时水位变化记为( )A、0.4 m B、0.6 m C、 D、2. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划“一带一路”地区覆盖总人口44亿,这个数用科学记数法表示为( )A、44×108 B、4.4×109 C、4.4×108 D、4.4×10103. 下列图形都是由完全相同的小正方形组成的,将它们分别沿虚线折叠后,不能围成一个小立方体的是( )A、
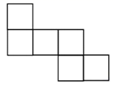 B、
B、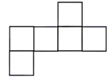 C、
C、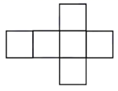 D、
D、 4. 下列说法正确的是( )A、单项式是整式,整式也是单项式 B、 与 是同类项 C、单项式 的系数是 ,次数是 D、 是一次二项式5. 下列解方程的步骤中正确的是( )A、由 ,可得 B、由 ,可得 C、由 ,可得 D、由 ,可得6. 有理数 按从小到大的顺序排列是( )A、 B、 C、 D、7. 如图 为北偏东30°方向, ,则 的方向为( )
4. 下列说法正确的是( )A、单项式是整式,整式也是单项式 B、 与 是同类项 C、单项式 的系数是 ,次数是 D、 是一次二项式5. 下列解方程的步骤中正确的是( )A、由 ,可得 B、由 ,可得 C、由 ,可得 D、由 ,可得6. 有理数 按从小到大的顺序排列是( )A、 B、 C、 D、7. 如图 为北偏东30°方向, ,则 的方向为( )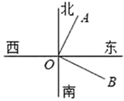 A、南偏东60° B、南偏东30° C、南偏西60° D、东偏北60°8. 如图,O是直线AB上一点,OP平分∠AOC,OQ平分∠BOC,则图中互余的角共有( )
A、南偏东60° B、南偏东30° C、南偏西60° D、东偏北60°8. 如图,O是直线AB上一点,OP平分∠AOC,OQ平分∠BOC,则图中互余的角共有( )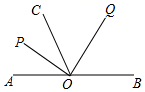 A、1对 B、2对 C、3对 D、4对9. 下列说法中错误的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则10. 某个工厂有技术工12人,平均每天每人可加工甲种零件24个或乙种零件15个,2个甲种零件和3个乙种零件可以配成一套,设安排 个技术工生产甲种零件,为使每天生产的甲乙零件刚好配套,则下面列出方程中正确的有( )个
A、1对 B、2对 C、3对 D、4对9. 下列说法中错误的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则10. 某个工厂有技术工12人,平均每天每人可加工甲种零件24个或乙种零件15个,2个甲种零件和3个乙种零件可以配成一套,设安排 个技术工生产甲种零件,为使每天生产的甲乙零件刚好配套,则下面列出方程中正确的有( )个① ②
③ ④
A、3 B、2 C、1 D、011. 某商店有两个进价不同的计算器都卖了80元,其中一个赢利60%,另一个亏本20%,在这次买卖中,这家商店( )A、赚了10元 B、赔了10元 C、赚了50元 D、不赔不赚12. 已知一列数:1,-2,3,-4,5,-6,7,…将这列数排成下列形式:第1行 1
第2行 -2 3
第3行 -4 5 -6
第4行 7 -8 9 -10
第5行 11 -12 13 -14 15
……
按照上述规律排下去,那么第100行从左边数第4个数是( )
A、-4954 B、4954 C、-4953 D、4953二、填空题
-
13. 写出一个次数为3的单项式,要求其中所含字母只有x,y: .14. 已知一个角的补角是它余角的3倍,则这个角的度数是度.15. 若m,n满足|m﹣6|+(7+n)2=0,则(m+n)2018= .16. 如图,剪去四边形的“一角”,得到一个五边形,这个五边形的周长一定这个四边形的周长(填“大于”,“小于”或“等于”),依据是.
 17. 钟表上4点30分时,时针与分针的夹角为 。18. 如图,长方形纸片 , 点E,F分别在边 , 上,连接 , 将对折B落在直线上的点处,得折痕;将对折,点A落在直线上的点得折痕 , 若 , 则 .
17. 钟表上4点30分时,时针与分针的夹角为 。18. 如图,长方形纸片 , 点E,F分别在边 , 上,连接 , 将对折B落在直线上的点处,得折痕;将对折,点A落在直线上的点得折痕 , 若 , 则 .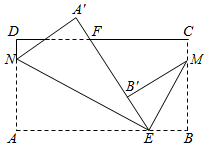 19. 规定: , , 例如 , .则式子的最小值是 .20. 程大位,明代珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).《算法统宗》中有这样一道题,其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两,请问:这一群人共有多少人?所分的银子共有多少两?若设共有x人,则可列方程为 .
19. 规定: , , 例如 , .则式子的最小值是 .20. 程大位,明代珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).《算法统宗》中有这样一道题,其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两,请问:这一群人共有多少人?所分的银子共有多少两?若设共有x人,则可列方程为 .
三、解答题
-
21. 计算:(1)、(2)、(3)、22. 先化简,再求值:(1)、 , 其中 , .(2)、 , 其中 , .23. 如图,OB、OC是 内部的两条射线, OM平分 ,ON平分 .
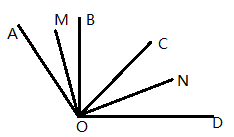 (1)、若 ,求 的度数;(2)、若 ,求 的度数(用含x的代数式表示)24. 如图: 、 、 、 四点在同一直线上.
(1)、若 ,求 的度数;(2)、若 ,求 的度数(用含x的代数式表示)24. 如图: 、 、 、 四点在同一直线上. (1)、若 ,
(1)、若 ,①比较线段的长短: (填“ ”、“ ”或“ ”);
②若 ,且 ,则 的长为 ;
(2)、若线段 被点 、 分成了 三部分,且 的中点 和 的中点 之间的距离是 ,求 的长.25. 一项工程,如果由甲工程队单独做需要20天完成,乙工程队单独做需要12天完成.现在由甲队单独做4天,剩下的工程由甲、乙合作完成.(1)、(列方程解答)剩下的部分合作还需要几天完成?(2)、若该工程的总费用为240万元,根据实际完成情况,甲乙两工程队各得多少万元?26. 如图,已知数轴上有三个点,它们表示的数分别是.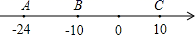 (1)、填空: , .(2)、若点A以每秒个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和7个单位长度的速度向右运动.试探索:的值是否随着时间t的变化而改变? 请说明理由。(3)、现有动点都从A点出发,点P以每秒个单位长度的速度向终点C移动:当点P移动到B点时,点Q才从A点出发,并以每秒个单位长度的速度向右移动,且当点P到达C点时,点Q就停止移动.设点P移动的时间为t秒,请试用含t的式了表示两点间的距离(不必写过程,直接写出结果).
(1)、填空: , .(2)、若点A以每秒个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和7个单位长度的速度向右运动.试探索:的值是否随着时间t的变化而改变? 请说明理由。(3)、现有动点都从A点出发,点P以每秒个单位长度的速度向终点C移动:当点P移动到B点时,点Q才从A点出发,并以每秒个单位长度的速度向右移动,且当点P到达C点时,点Q就停止移动.设点P移动的时间为t秒,请试用含t的式了表示两点间的距离(不必写过程,直接写出结果).