(沪教版)2022-2023学年度第一学期六年级数学4.4 扇形的面积 同步测试
试卷更新日期:2022-07-19 类型:同步测试
一、单选题
-
1. 莱洛三角形,也译作勒洛三角形或圆弧三角形,它的应用广泛,不仅用于建筑、商品的外包装设计,还用在工业方面.莱洛三角形形状的钻头可钻出正方形的孔,发动机的原件上也有莱洛三角形,如图1.别以等边 的顶点A,B,C为圆心,以 长为半径画弧,我们把这三条弧组成的封闭图形就叫做莱洛三角形,如图2.若 ,则莱洛三角形的面积(即阴影部分面积)为( )
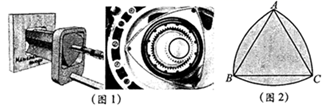 A、 B、 C、 D、2. 如图,在 中, , 的半径为3,则图中阴影部分的面积是( )
A、 B、 C、 D、2. 如图,在 中, , 的半径为3,则图中阴影部分的面积是( )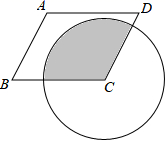 A、 B、 C、 D、3. 如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD , 图中阴影为重合部分,则阴影部分的面积为( )
A、 B、 C、 D、3. 如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD , 图中阴影为重合部分,则阴影部分的面积为( )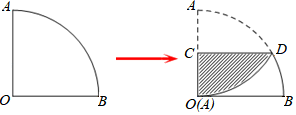 A、6π﹣ B、6π﹣9 C、12π﹣ D、4. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为 ,则图中阴影部分的面积是( )
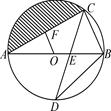
A、6π﹣ B、6π﹣9 C、12π﹣ D、4. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为 ,则图中阴影部分的面积是( ) A、 B、 C、 D、5. 如图,⊙O的直径AB=2,C是弧AB的中点,点E是∆ABC的内心,以E为圆心,AE为半径作扇形EAB,π取3,则阴影部分的面积为( )
A、 B、 C、 D、5. 如图,⊙O的直径AB=2,C是弧AB的中点,点E是∆ABC的内心,以E为圆心,AE为半径作扇形EAB,π取3,则阴影部分的面积为( )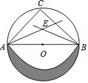 A、 B、 C、 D、6. 今年寒假期间,小明参观了中国扇博物馆,如图是她看到的纸扇和团扇. 已知纸扇的骨柄长为30cm,扇面有纸部分的宽度为18cm,折扇张开的角度为150°,若这两把扇子的扇面面积相等,则团扇的半径为( )
A、 B、 C、 D、6. 今年寒假期间,小明参观了中国扇博物馆,如图是她看到的纸扇和团扇. 已知纸扇的骨柄长为30cm,扇面有纸部分的宽度为18cm,折扇张开的角度为150°,若这两把扇子的扇面面积相等,则团扇的半径为( ) A、 B、 C、 D、7. 如图,在Rt△ABC中,∠ABC=90°,AB= ,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
A、 B、 C、 D、7. 如图,在Rt△ABC中,∠ABC=90°,AB= ,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )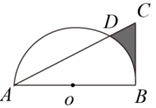 A、 B、 C、 D、8. 如图,圆锥的底面半径r=6,高h=8,则圆锥的侧面积是( )
A、 B、 C、 D、8. 如图,圆锥的底面半径r=6,高h=8,则圆锥的侧面积是( )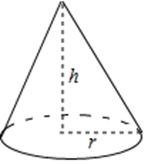 A、15π B、30π C、45π D、60π9. 如图, 中, , , ,则阴影部分的面积是( )
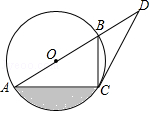
A、15π B、30π C、45π D、60π9. 如图, 中, , , ,则阴影部分的面积是( )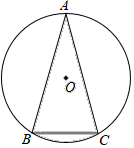 A、 B、 C、 D、10. 已知点C、D是以AB为直径的半圆的三等分点,弧CD的长为 ,则图中阴影部分的面积为( )
A、 B、 C、 D、10. 已知点C、D是以AB为直径的半圆的三等分点,弧CD的长为 ,则图中阴影部分的面积为( )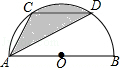 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在⊙O中,OA=2,∠C=45°,则图中阴影部分的面积为 .
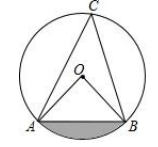 12. 如图,长方形ABCD中,AB=2,AD=6,以点B为圆心,AB长为半径画圆交BC于点F,以点D为圆心,AD长为半径画圆交DC的延长线于点E,则图中阴影部分面积为.
12. 如图,长方形ABCD中,AB=2,AD=6,以点B为圆心,AB长为半径画圆交BC于点F,以点D为圆心,AD长为半径画圆交DC的延长线于点E,则图中阴影部分面积为.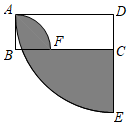 13. 在一个圆中任意画三条半径,可以把这个圆分成个不同的扇形.14. 若扇形的圆心角为120°,半径为4,则该扇形的面积为.15. 如图,将一块含 角的直角三角板和半圆形量角器按如图的方式摆放,使三角板斜边与半圆相切,若半径 ,则图中阴影部分的面积是 . (结果保留π)
13. 在一个圆中任意画三条半径,可以把这个圆分成个不同的扇形.14. 若扇形的圆心角为120°,半径为4,则该扇形的面积为.15. 如图,将一块含 角的直角三角板和半圆形量角器按如图的方式摆放,使三角板斜边与半圆相切,若半径 ,则图中阴影部分的面积是 . (结果保留π)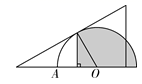
三、解答题
-
16. 一个扇形的圆心角60°,半径为12cm,求它的面积.(保留π)17. 如图,直角三角形△ABC的直角顶点为C,且AC=5,BC=12,AB=13,将此三角形绕点A顺时针旋转90°到直角三角形AB′C′的位置.(结果保留π)
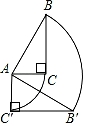 (1)、求运动过程中点B和点C经过的路径之和;(2)、求△ABC扫过的面积.18. 如图,AB是圆锥底面圆的直径,SO是高,OA=3cm , SO=4cm , 求圆锥侧面展开图的面积.
(1)、求运动过程中点B和点C经过的路径之和;(2)、求△ABC扫过的面积.18. 如图,AB是圆锥底面圆的直径,SO是高,OA=3cm , SO=4cm , 求圆锥侧面展开图的面积.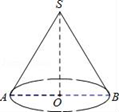 19. 如图所示,∠AOB=90°,∠COB=45°。
19. 如图所示,∠AOB=90°,∠COB=45°。 (1)、已知OB=10,求以OB为直径的半圆面积及扇形COB的面积;(结果可保留π)(2)、填空:已知阴影甲的面积为6平方厘米,则阴影乙的面积为平方厘米。20. 如图,求边长为10的正方形中阴影部分的周长和面积。
(1)、已知OB=10,求以OB为直径的半圆面积及扇形COB的面积;(结果可保留π)(2)、填空:已知阴影甲的面积为6平方厘米,则阴影乙的面积为平方厘米。20. 如图,求边长为10的正方形中阴影部分的周长和面积。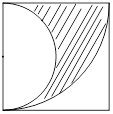 21. 钟面上扇形(涂色部分)的圆心角各是多少度?
21. 钟面上扇形(涂色部分)的圆心角各是多少度?①
 ;
;②
 ;
;③
 。22. 小明在一个直径6厘米的圆中画一个圆心角是60°的扇形,这个扇形的大小是圆的几分之几。要使扇形的大小正好是圆的 ,它的圆心角应是多少度?
。22. 小明在一个直径6厘米的圆中画一个圆心角是60°的扇形,这个扇形的大小是圆的几分之几。要使扇形的大小正好是圆的 ,它的圆心角应是多少度?
四、综合题