（沪教版）2022-2023学年度第一学期六年级数学4.3 圆的面积同步测试

试卷更新日期：2022-07-19 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，⊙O₁的弦AB是⊙O₂的切线，且AB∥O₁O₂ ，如果AB＝12cm，那么阴影部分的面积为（）.

A、36πcm² B、12πcm² C、8πcm² D、6πcm²

查看试题解析
2. 一个圆的半径为2cm，则它的面积是（）（ $π$ 取3.14）．

A、6.28cm B、12.56cm C、 $12.56 c m^{2}$ D、 $6.28 c m^{2}$

查看试题解析
3. 如图，已知在Rt△ABC中，E，F分别是边AB，AC上的点， $A E = \frac{1}{3} A B$ ， $A F = \frac{1}{3} A C$ ，分别以BE、EF、FC为直径作半圆，面积分别为S₁ ， S₂ ， S₃ ，则S₁ ， S₂ ， S₃之间的关系是（）

A、S₁+S₃＝2S₂ B、S₁+S₃＝4S₂ C、S₁＝S₃＝S₂ D、 $S_{2} = \frac{1}{3} (S_{1} + S_{3})$

查看试题解析
4. 圆桌面（桌面中间有一个直径为1m的圆洞）正上方的灯泡（看作一个点）发出的光线照射平行于地面的桌面后，在地面上形成如图所示的圆环形阴影．已知桌面直径为2m，桌面离地面1m，若灯泡离地面2m，则地面圆环形阴影的面积是（）

A、2πm² B、3πm² C、6πm² D、12πm²

查看试题解析
5. 周长相等的长方形、正方形和圆，（）面积最大．

A、长方形 B、正方形 C、圆 D、无法确定

查看试题解析
6. 我国古代数学著作《增删算法统宗》记载“圆中方形”问题：“今有圆田一段，中间有个方池，丈量田地待耕犁，恰好三分在记，池面至周有数，每边三步无疑，内方圆径若能知，堪作算中第一”其大意为：有一块圆形的田，中间有一块正方形水池，测量出除水池外圆内可耕地的面积恰好72平方步，从水池边到圆周，每边相距3步远.如果你能求出正方形的边长是 $x$ 步，则列出的方程是（）

A、 $π {(x + 3)}^{2} - x^{2} = 72$ B、 $π {(\frac{x}{2} + 3)}^{2} - x^{2} = 72$ C、 $π {(x + 3)}^{2} - x^{2} = 36$ D、 $π {(\frac{x}{2} + 3)}^{2} - x^{2} = 36$

查看试题解析
7. 如图，正方形 $A B C D$ 内的图形来自中国古代的太极图，正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称，设正方形 $A B C D$ 的面积为 $S$ ，黑色部分面积为 $S_{1}$ ，则 $S_{1} ： S$ 的比值为（）

A、 $\frac{π}{8}$ B、 $\frac{π}{4}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
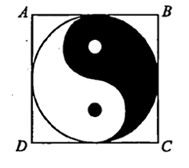8. 如图，△ABC中，AB＝AC，AD是∠BAC的平分线，F是AC的中点，过点F作EF⊥AC交AB于点E，交AD于点O.若OA＝3，则△ABC外接圆的面积为（）

A、3π B、4π C、6π D、9π

查看试题解析
9. 如图所示，分别以Rt△ABC(三条边分别为a，b，c)的三边为边长向外作正方形，然后分别以三个正方形的中心为圆心、正方形边长的一半为半径作圆．若这三个圆的面积分别为S₁ ， S₂ ， S₃(S₁>S₂>S₃)，则这三个圆的面积之间的关系为（）

A、S₁=S₂+S₃ B、S₁>S₂+S₃ C、S₁≥S₂+S₃ D、不能确定

查看试题解析
10. 如果大圆的周长是小圆周长的4倍，那么小圆面积是大圆面积的（）。

A、 $\frac{1}{4}$ B、 $\frac{1}{5}$ C、 $\frac{1}{16}$ D、 $\frac{1}{25}$

查看试题解析

二、填空题

11. 如图，某环形绿化带的外圆半径为6.5m，内圆半径为3.5m，现有一块宽为6m的长方形绿化带面积与该圆环绿化带面积相同，则长方形绿化带的长为m．（结果保留 $π$ ）

查看试题解析
12. 2022年中国举办了第二十四届冬季奥林匹克运动会，冬奥会火炬外壳采用了重量轻、耐高温的碳纤维及其复合材料制造而成，具有“轻、固、美”的特点 .已知某种成型的碳纤维直径约6微米（1微米= $1 0^{- 6}$ 米），这种碳纤维的横截面的面积约为米²（ $π \approx$ 3.14，结果用科学记数法表示） .

查看试题解析
13. 如图，C是线段AB上的任一点，分别以AB.AC.BC为直径在线段AB同侧作半圈，则这三个半圆周围成的图形被阿基米德称为“鞋匠刀形”（即图中阴影部分）.当“鞋匠刀形”的面积等于以BC为直径的半圆的面积时，过C作CD⊥AB，交圆周于点D，连接BD，则 $\frac{C D}{B C}$ 的值为.

查看试题解析
14. 刘徽是我国魏晋时期卓越的数学家，他在《九章算术》中提出了“割圆术”利用圆的内接正多边形逐步逼近圆来近似计算圆的面积，他从正六边形开始分割圆，每次边数成倍增加，依次可得圆内接正十二边形，内接正二十四边形……割的越细，圆的内接正多边形就越接近圆.如图，若用圆的内接正十二边形的面积S₁ ，来近似估计⊙O的面积S，设正十二边形边长为1，则S₁=； $\frac{S}{S_{1}} =$ .

查看试题解析
15. 如图，已知 $⊙ O$ 的两条直径 $A B$ ， $E F$ 互相垂直， $\overset{⌢}{C E D}$ 和 $\overset{⌢}{C F D}$ 所对的圆心角都为 $12 0^{°}$ ，且 $\overset{⌢}{C E D} = \overset{⌢}{C F D}$ .现随机地向该图形内掷一枚小针，记针尖落在 $\overset{⌢}{C E D}$ 和 $\overset{⌢}{C F D}$ 所围封闭区域内的概率为 $P_{1}$ ，针尖落在 $⊙ O$ 内的概率为 $P_{2}$ ，则 $\frac{P_{1}}{P_{2}} =$ .

查看试题解析

三、解答题

16. 为庆祝中国共产党的百年华诞，某校要进行美化校园，各班同学设计热爱祖国的板报．八年一班学生在设计板报时，在黑板中间画一个半径为R的大圆，然后挖去半径为r的四个小圆，分别作为热爱中国共产党、热爱人民、认同中华文化和继承革命传统四个学习区域．请计算当R＝7.8cm，r＝1.1cm时剩余部分的面积．（结果保留π）

查看试题解析
17. 如图，在面积为2平方米的正方形ABCD的木料中，挖去以边BC为直径的半圆，则剩下的木料的面积为多少平方米？（ $π \approx 3.14$ ，结果精确到 $0.1$ ）

查看试题解析
18. 如图，已知阴影部分面积为100平方厘米，求圆环的面积。（π取3.14）

查看试题解析
19. 认真算一算（π取3.14）

(1)、求图1中阴影部分的周长。

(2)、求图2中阴影部分的面积。

查看试题解析
20. 如图，在半径为R的圆形钢板上，冲去半径为r的四个小圆，若R＝8cm，r＝1cm，请你计算剩余部分面积(结果保留π).

查看试题解析
21. 某小区设计的花坛形状如图中的阴影部分，已知AB 和CD所在圆心都是点O，
请同学们解决以下两个问题∶

(1)、若OC=2m，AC=3m， $∠ O$ =120°时，求花坛的周长和面积（结果保留π）

(2)、阅读材料∶两个数的平方的差可以表示为这两个数的和与这两个数的差的积。
即∶ $a^{2} - b^{2} = (a + b) (a - b)$ ，例如75²-25²=（75+25）（75-25）=100×50=5000；

在求解面积时，有位同学发现扇形面积公式∶S_扇= $\frac{1}{2} l r$ ，类似于三角形面积公式；

于是他突发奇想，类比梯形面积公式，得到花坛面积∶S = $\frac{1}{2} （ l_{1} + l_{2}) d$ ，此时d=AC，结合阅读材料和扇形面积推导过程思考他的猜想正确吗?如果正确，请写出推导过程；如果不正确，请说明理由。

查看试题解析
22. 如图所示，较大的半圆半径 $r_{大} = 5$ ，较小的半圆半径 $r_{小} = 3$ ，求阴影部分的周长 $C_{阴影}$ 和面积 $S_{阴影}$ ．（π取3.14）

查看试题解析
23. 如图两个半圆的直径分别在正方形的一组对边上，用代数式表示图中阴影部分的面积．并计算当x＝4时，阴影部分的面积（x取3.14）．

查看试题解析
24. 一个运动场如下图，两端是半圆形，中间是长方形.这个运动场的周长和面积分别是多少?

查看试题解析

（沪教版）2022-2023学年度第一学期六年级数学4.3 圆的面积 同步测试

一、单选题

二、填空题

三、解答题

（沪教版）2022-2023学年度第一学期六年级数学4.3 圆的面积同步测试