(沪教版)2022-2023学年度第一学期六年级数学4.2 弧长 同步测试
试卷更新日期:2022-07-19 类型:同步测试
一、单选题
-
1. 如图,将边长为1的菱形绕点A旋转,当B,C两点恰好落在扇形的上时,的长度等于( )
 A、 B、 C、 D、2. 用半径为 ,圆心角为 的扇形纸片恰好能围成一个圆锥的侧面,则这个圆锥底面半径为( )A、 B、 C、 D、3. 如图, 中, , , ,点 从 点出发,沿 运动到点 停止,过点 作射线 的垂线,垂足为 ,点 运动的路径长为( )
A、 B、 C、 D、2. 用半径为 ,圆心角为 的扇形纸片恰好能围成一个圆锥的侧面,则这个圆锥底面半径为( )A、 B、 C、 D、3. 如图, 中, , , ,点 从 点出发,沿 运动到点 停止,过点 作射线 的垂线,垂足为 ,点 运动的路径长为( )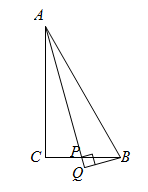 A、 B、 C、 D、4. 如图, , , 是半径为 的 上的三点,如果 ,那么 的长为( )
A、 B、 C、 D、4. 如图, , , 是半径为 的 上的三点,如果 ,那么 的长为( )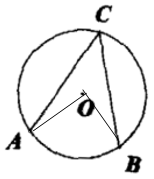 A、π B、 C、 D、5. 如图, 与 切于点 , , 是 上一点,连接 并延长与 交于点 ,连接 ,
A、π B、 C、 D、5. 如图, 与 切于点 , , 是 上一点,连接 并延长与 交于点 ,连接 ,, ,则 的长为( )
 A、 B、 C、 D、6. 如图,⊙O的半径为4,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点,过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P从点A运动到点D时,点Q所经过的路径长为( )
A、 B、 C、 D、6. 如图,⊙O的半径为4,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点,过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P从点A运动到点D时,点Q所经过的路径长为( ) A、 B、 C、 D、7. 如图,AB切⊙O于点B,OA=2 ,AB=3,弦BC∥OA,则劣弧BC的长度为( )
A、 B、 C、 D、7. 如图,AB切⊙O于点B,OA=2 ,AB=3,弦BC∥OA,则劣弧BC的长度为( ) A、 B、 C、π D、8. 如图,若用圆心角为120°,半径为9的扇形围成一个圆锥侧面(接缝忽略不计),则这个锥的底面直径是( )
A、 B、 C、π D、8. 如图,若用圆心角为120°,半径为9的扇形围成一个圆锥侧面(接缝忽略不计),则这个锥的底面直径是( )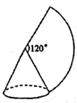 A、6 B、3 C、9 D、129. 圆锥的母线长为9cm,底面圆的直径为10cm,那么这个圆锥的侧面展开图的圆心角度数是( )
A、6 B、3 C、9 D、129. 圆锥的母线长为9cm,底面圆的直径为10cm,那么这个圆锥的侧面展开图的圆心角度数是( ) A、150° B、200° C、180° D、240°10. 已知圆的半径为3,扇形的圆心角为120°,则扇形的弧长为( )A、 B、 C、 D、
A、150° B、200° C、180° D、240°10. 已知圆的半径为3,扇形的圆心角为120°,则扇形的弧长为( )A、 B、 C、 D、二、填空题
-
11. 一个扇形的弧长是18π,圆心角是108度,则此扇形的半径是 cm.12. 一段弧所在的圆的周长为12厘米,弧所对的圆心角为 60°,那么这段弧的长为米。13. 已知圆中40°圆心角所对的弧长为3π,则这个圆的周长。14. 如图①是山东舰航徽的构图,采用航母45度破浪而出的角度,展现山东舰作为中国首艘国产舰母橫空出世的气势,将舰徽中第一条波浪抽象成几何图形,则是一条长为 的弧,若该弧所在的扇形是高为12的圆锥侧面展开图(如图②),则该圆锥的母线长 为 .
 15. 如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则 的长为 .
15. 如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则 的长为 .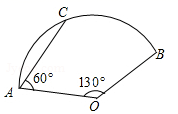
三、解答题
-
16. 已知半圆的直径CD=12cm,如图所示,弧DE所对的圆心角∠ECD=30°,求阴影部分的周长.
 17. 如图,在单位长为1的网格图中,画出格点△ABC绕点A按逆时针方向旋转90°后的△AB'C′;并求出点C所经过的路线长.
17. 如图,在单位长为1的网格图中,画出格点△ABC绕点A按逆时针方向旋转90°后的△AB'C′;并求出点C所经过的路线长. 18. 在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
18. 在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点). (1)、画出△ABC向下平移4个单位后的△A1B1C 1 , 并直接写出△ABC在平移过程中扫过的面积;(2)、画出△ABC绕点O顺时针旋转90°后的△A2B2C2 , 并直接写出点A旋转到A2所经过的路线长.
(1)、画出△ABC向下平移4个单位后的△A1B1C 1 , 并直接写出△ABC在平移过程中扫过的面积;(2)、画出△ABC绕点O顺时针旋转90°后的△A2B2C2 , 并直接写出点A旋转到A2所经过的路线长.四、综合题
-
19. 已知 的两边分别与圆O相切于点A,B,圆O的半径为r.
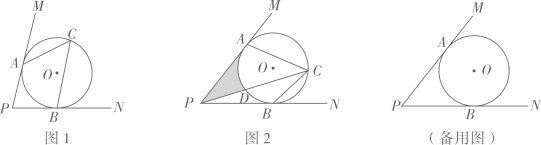 (1)、如图1,点C在点A,B之间的优弧上, ,求 的度数;(2)、如图2,点C在圆上运动,当 最大时,要使四边形 为菱形, 的度数应为多少?请说明理由;(3)、若 交圆O于点D,求第(2)问中对应的阴影部分的周长(用含r的式子表示).20. 如图,在等腰△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E。
(1)、如图1,点C在点A,B之间的优弧上, ,求 的度数;(2)、如图2,点C在圆上运动,当 最大时,要使四边形 为菱形, 的度数应为多少?请说明理由;(3)、若 交圆O于点D,求第(2)问中对应的阴影部分的周长(用含r的式子表示).20. 如图,在等腰△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E。 (1)、求证:DE是⊙O的切线;(2)、若DE= ,∠C=30°,求AD的长。21. 如图,在△ABC中,AB=AC,O是边AC上的点,以OC为半径的圆分别交边BC、AC于点D、E,过点D作DF⊥AB于点F.
(1)、求证:DE是⊙O的切线;(2)、若DE= ,∠C=30°,求AD的长。21. 如图,在△ABC中,AB=AC,O是边AC上的点,以OC为半径的圆分别交边BC、AC于点D、E,过点D作DF⊥AB于点F. (1)、求证:直线DF是⊙O的切线;(2)、若OC=1,∠A=45°,求劣弧DE的长.22. 如图, 中, ,以 为直径的 交 边于点 ,连接 ,过 作 的垂线,交 边于点 ,交 边的延长线于点 .
(1)、求证:直线DF是⊙O的切线;(2)、若OC=1,∠A=45°,求劣弧DE的长.22. 如图, 中, ,以 为直径的 交 边于点 ,连接 ,过 作 的垂线,交 边于点 ,交 边的延长线于点 . (1)、求证: 是 的切线;(2)、若 , ,求劣弧 的长.
(1)、求证: 是 的切线;(2)、若 , ,求劣弧 的长.

