（沪教版）2022-2023学年度第一学期六年级数学3.6 等可能事件 同步测试
试卷更新日期：2022-07-19 类型：同步测试
一、单选题
-
1. 某校九年级选出三名同学参加学校组织的“法治和安全知识竞赛”.比赛规定，以抽签方式决定每个人的出场顺序，主持人将表示出场顺序的数字1，2，3分别写在3张同样的纸条上，并将这些纸条放在一个不透明的盒子中，搅匀后从中任意抽出一张，小星第一个抽，下列说法中正确的是（ ）A、小星抽到数字1的可能性最小 B、小星抽到数字2的可能性最大 C、小星抽到数字3的可能性最大 D、小星抽到每个数的可能性相同2. 在一个不透明的布袋内，有红球5个，黄球4个，白球1个，蓝球3个，它们除颜色外，大小、质地都相同.若随机从袋中摸取一个球，则摸中哪种球的概率最大（ ）A、红球 B、黄球 C、白球 D、蓝球3. 在同一副扑克牌中抽取2张“黑桃”，5张“梅花”，3张“方块”．将这10张牌背面朝上，从中任意抽取1张，是“方块”的概率为（ ）A、 B、 C、 D、4. 一个不透明的袋中，装有2个黄球，3个红球和5个白球，它们除颜色外都相同．从袋中任意摸出一个球，是黄球的概率是（ ）A、 B、 C、 D、5. 篮球裁判员通常用抛掷硬币的方式来确定哪一方先选场地，那么抛掷一枚均匀的硬币一次，正面朝上的概率是（ ）A、1 B、 C、 D、6. 如图是一个游戏转盘．自由转动转盘，当转盘停止转动后，指针落在数字1，2，3，4所示区域内可能性最大的是（ )
A、1号 B、2号 C、3号 D、4号7. 下列成语或词语所反映的事件中，发生的可能性最小的是（ ）A、瓜熟蒂落 B、守株待兔 C、旭日东升 D、瓮中捉鳖8. “14人中至少有2人在同一个月过生日”这一事件发生的概率为P，则（ ）A、P＝0 B、0＜P＜1 C、P＝1 D、P＞19. 下列说法不正确的是（ ）A、通过大量重复试验，可以用频率估计概率 B、概率很小的事件不可能发生 C、必然事件发生的概率是1 D、投一枚图钉，“钉尖朝上”的概率不能用列举法计算10. 如图是一个4×4的方格，若在这个方格内投掷飞镖，则飞镖恰好落在阴影部分的概率是（ ）
A、 B、 C、 D、二、填空题
-
11. 老师为帮助学生正确理解物理变化与化学变化，将6种生活现象制成看上去无差别卡片（如图）．从中随机抽取一张卡片，抽中生活现象是物理变化的概率是
12. 有5张无差别的卡片，上面分别标有-2，｜-2｜，（-2）2 ， -（-2）0 ， （-2）-2 ， 从中随机抽取1张，则抽取的卡片上的数是正数的概率是13. 一个人做抛硬币实验，连续9次都得到正面朝上，则第10次得到正面朝上的概率是14. 不透明的袋子中装有4个红球、3个黄球和5个蓝球，每个球除颜色不同外其它都相同，从中任意摸出一个球球的可能性最大.15. 已知四张牌的正面如图所示，背面完全相同，将它们正面朝下洗匀后放在桌上，从中随机抽出一张，牌面数字恰好为偶数的概率是.
三、解答题
-
16. 在一个不透明的口袋中装有1个红球，1个绿球和1个白球，这3个球除颜色不同外，其它都相同，从口袋中随机摸出1个球，记录其颜色．然后放回口袋并摇匀，再从口袋中随机摸出1个球，记录其颜色，请利用画树状图或列表的方法，求两次摸到的球都是红球的概率．17. 下列第一排表示各盒中球的情况，第二排的语言描述了摸到篮球的可能性大小，请你用线把第一排盒子与第二排的描述连接起来使之相符．
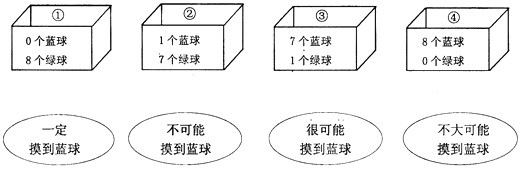18. 某商场为了吸引顾客，设立了一个可以自由转动的转盘（转盘被等分成
个扇形，如图）并规定：顾客在本商场每消费 
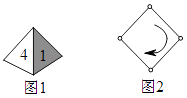
元，就能获得一次转动转盘的机会，如果转盘停止后，指针正好对准红、黄或绿色区域，顾客就可以分别获得 100 元、 50 元、 20 元的购物券．某顾客消费 210 元，他转动转盘获得购物券的概率是多少?他得到 100 元、 50 元、 20 元购物券的概率分别是多少?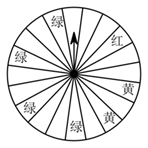 
19. 如图1，一枚质地均匀的正四面体骰子，它有四个面．并分别标有数字1，2，3，4．如图2，正方形ABCD顶点处各有一个圈．跳圈游戏的规则为：游戏则每掷一次骰子，骰子着地一面上的数字是几，就沿正方形的边顺时针方向连续跳几个边长．如：若从圈A起跳，第一次掷得3，就顺时针连续跳3个边长，落到圈D．若第二次掷得2，就从D开始顺时针连续跳2个边长，落到圈B．…设游戏这从圈A起跳．嘉嘉随机掷一次骰子．淇淇随机掷两次骰子．请问嘉嘉与淇淇掷完骰子落回到圈A的可能性一样吗？回答问题并说明理由．
20. 在不透明的袋子中装有3个红球和5个黄球，每个球除颜色外都相同，从中任意摸出一个球（1）摸到哪种颜色球的可能性大？
（2）请你通过改变袋子中某一种颜色球的数量，设计一种方案；使“摸出红球”和“摸出黄球”的可能性大小相同．
21. 学科内综合题：现把10个数：﹣1，23，15，12，0，﹣31，﹣11，29，43，﹣62．分别写在10张纸条上，然后把纸条放进外形，颜色完全相同的小球内，再把这10个小球放进一个大玻璃瓶中，从中任意取一球，得到正数的可能性与得到负数的可能性哪个大．22. 一只不透明的袋子中有2个红球，3个绿球和5个白球，每个球除颜色外都相同，将球搅匀，从中任意摸出一个球．（1）会有哪些可能的结果？
（2）你认为摸到哪种颜色的球的可能性最大？哪种颜色的球的可能性最小？
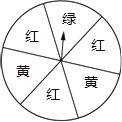
23.有一个转盘（如图所示），被分成6个相等的扇形，颜色分为红、绿、黄三种，指针的位置固定，转动转盘后任其自由停止，其中的某个扇形会恰好停在指针所指的位置（指针指向两个扇形的交线时，重新转动）．下列事件：①指针指向红色；②指针指向绿色；③指针指向黄色；④指针不指向黄色．估计各事件的可能性大小，完成下列问题：
（1）可能性最大和最小的事件分别是哪个？（填写序号）
（2）将这些事件的序号按发生的可能性从小到大的顺序排列： ．
24. 在5个不透明的袋子中分别装有10个球，其中，1号袋中有10个红球，2号袋中有8红2白球，3号袋中有5红5白球，4号袋中有1红9白球，5号袋中有10个白球，从各个袋子中摸到白球的可能性一样吗？请将袋子的序号按摸到白球的可能性从小到大的顺序排列．