（人教版）2022-2023学年度第一学期八年级数学15.2.1 分式的乘除同步测试

试卷更新日期：2022-07-19 类型：同步测试

进入出卷网下载

一、单选题

1. 计算 $\frac{x}{a + 1} \cdot \frac{a^{2} - 1}{2 x}$ 的结果正确的是（）

A、 $\frac{a - 1}{2}$ B、 $\frac{a + 1}{2}$ C、 $\frac{a - 1}{2 x}$ D、 $\frac{a + 1}{2 a + 2}$

查看试题解析
2. 化简 $x \div \frac{x}{y} \cdot \frac{1}{x}$ 结果为（）

A、 $\frac{x}{y}$ B、 $\frac{y}{x}$ C、 $x y$ D、1

查看试题解析
3. 下列计算正确的是（）

A、（ $\frac{b}{a}$ ）³ $= \frac{b^{3}}{a}$ B、 $\frac{- a - b}{a - b} = - 1$ C、 $\frac{1}{a} + \frac{2}{b} = \frac{3}{a + b}$ D、a² $\div \frac{1}{a} =$ a³

查看试题解析
4. 某数学老师模仿学生喜欢的《王牌对王牌》节目在课堂上设计了一个接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算得到结果，再将计算结果传递给下一人，最后完成化简．过程如图所示，接力中，自己负责的那一步出现错误的是（）

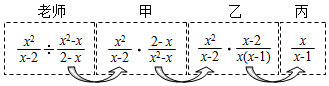A、只有乙 B、只有丙 C、甲和丙 D、乙和丙

查看试题解析
5. 约分： $- 3 x y^{2} \cdot \frac{2 x}{18 y^{3}} =$ （）

A、 $- \frac{x^{2}}{3 y}$ B、 $- \frac{x^{2}}{y}$ C、 $- \frac{x^{2}}{3 y^{2}}$ D、 $- \frac{x}{3 y}$

查看试题解析
6. 下列计算：① $\frac{x - y}{x^{2} - y^{2}} = \frac{1}{x - y}$ ；② $\frac{y}{x} \div \frac{x}{y} \cdot (- \frac{y}{x}) = - \frac{y}{x}$ ；③ $\frac{{(a - b)}^{2}}{{(a + b)}^{2}} = - 1$ ；④ $\frac{a^{2} + a b}{a - b} \div \frac{a b}{a - b} = \frac{a + b}{b}$ ；其中结果正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 若 $\times x y = 3 x^{2} y + 2 x y$ ，则内应填的式子是（）

A、 $3 x + 2$ B、 $x + 2$ C、3 $x y + 2$ D、 $x y + 2$

查看试题解析
8. 已知 $\frac{2 x}{x^{2} - y^{2}} \div M = \frac{1}{x - y}$ ，则M等于（）

A、 $\frac{2 x}{x + y}$ B、 $\frac{x + y}{2 x}$ C、 $\frac{2 x}{x - y}$ D、 $\frac{x - y}{2 x}$

查看试题解析
9. 使式子 $\frac{x + 3}{x - 3}$ ÷ $\frac{x + 5}{x - 4}$ 有意义的x值是（）

A、x≠3，且x≠﹣5 B、x≠3，且x≠4 C、x≠4且 x≠﹣5 D、x≠3，且x≠4且x≠﹣5

查看试题解析
10. 如图，设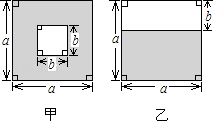k= $\frac{甲图中阴影部分面积}{乙图中阴影部分面积}$ （a＞b＞0），则有（）

A、k＞2 B、1＜k＜2 C、 $\frac{1}{2} < k < 1$ D、 $0 < k < \frac{1}{2}$

查看试题解析

二、填空题

11. $- \frac{2 a}{b^{2}}$ = $2 a$ ÷ ．

查看试题解析
12. 计算： $(\frac{- 2 a^{2} b}{3 c})^{2} \div (\frac{2 a b}{3 c})^{3} =$ ．

查看试题解析
13. 计算： $\frac{6}{a^{2} - 9} \div \frac{1}{a + 3} =$ ．

查看试题解析
14. 小明在进行两个多项式的乘法运算时，不小心把乘以 $\frac{x + y}{2}$ 错抄成乘以 $\frac{x}{2}$ ，结果得到(x²-xy)，则正确的计算结果是。

查看试题解析
15. 化简 $\frac{a^{2} - 9}{2 a - 4}$ ÷ $\frac{a + 3}{2 - a}$ 的结果为．

查看试题解析

三、解答题

16. 计算： $\frac{3 a}{4 b} \cdot \frac{16 b}{9 a^{2}}$ ，

查看试题解析
17. 已知x³﹣x²﹣x+1=（x﹣1）（x²﹣1）且x是整数，求证： $\frac{x^{3} - x^{2} - x + 1}{x^{2} - 2 x + 1}$ 是整数．

查看试题解析
18. 若a＞0，M= $\frac{a + 1}{a + 2}$ ， N= $\frac{a + 2}{a + 3}$ ，猜想M与N的大小关系，并证明你的猜想．

查看试题解析
19. 因城市建设的需要，某市将长方形广场的一边增加12米，另一边减少12米，变成边长为a米的正方形广场，试问改建前后广场的面积比是多少？面积变大了吗？

查看试题解析
20. 已知 $y_{1} = 2 x ， y_{2} = \frac{2}{y_{1}} ， y_{3} = \frac{2}{y_{2}} ， \dots ， y_{2018} = \frac{2}{y_{2017}}$ ，求 $y_{1} \cdot y_{2018}$ 的值.

查看试题解析
21. 化简运用：小丽在求解一个有解的分式方程 $\frac{x^{2} - 1}{x^{2} - 2 x + 1} \div \frac{x + 1}{x - 1} \cdot \frac{1 - x}{1 + x}$ ＝▓时，将等号右边的值写错，又找不到原题目了，但肯定的是“▓”为三个“有理数的特殊数”﹣1，0，1中的一个，请你帮她确认这个数.并求出原分式方程的解（提示：先化简分式再求解方程可不写出确认“▓”的过程，但要写出解方程的过程）.

查看试题解析
22. 先化简 $(\frac{x + 2}{x} - \frac{x - 1}{x - 2}) \div \frac{x - 4}{x^{2} - 4 x + 4}$ ，再从 $- 2 < x \leq 2$ 中选择适当的数代入求值．

查看试题解析
23. （Ⅰ）计算：（a﹣b）（a²+ab+b²）
（Ⅱ）利用所学知识以及（Ⅰ）所得等式，化简代数式 $\frac{m^{3} - n^{3}}{m^{2} + m n + n^{2}}$ ÷ $\frac{m^{2} - n^{2}}{m^{2} + 2 m n + n^{2}}$ ．

查看试题解析
24. 阅读下面的解题过程:
已知 $\frac{x}{x^{2} + 1}$ = $\frac{1}{3}$ ,求 $\frac{x^{2}}{x^{4} + 1}$ 的值.
解:由 $\frac{x}{x^{2} + 1}$ = $\frac{1}{3}$ 知x≠0,所以 $\frac{x^{2} + 1}{x}$ =3,即x+ $\frac{1}{x}$ =3.所以
$\frac{x^{4} + 1}{x^{2}}$ =x²+ $\frac{1}{x^{2}}$ = ${(x + \frac{1}{x})}^{2}$ -2=3²-2=7.
故 $\frac{x^{2}}{x^{4} + 1}$ 的值为 $\frac{1}{7}$ .
该题的解法叫做“倒数求值法”,请你利用“倒数求值法”解下面的题目:
若 $\frac{x}{x^{2} - 3 x + 1}$ = $\frac{1}{5}$ ,求 $\frac{x^{2}}{x^{4} + x^{2} + 1}$ 的值.

查看试题解析

（人教版）2022-2023学年度第一学期八年级数学15.2.1 分式的乘除 同步测试

一、单选题

二、填空题

三、解答题

（人教版）2022-2023学年度第一学期八年级数学15.2.1 分式的乘除同步测试