（人教版）2022-2023学年度第一学期八年级数学14.2.2 完全平方公式同步测试

试卷更新日期：2022-07-19 类型：同步测试

进入出卷网下载

一、单选题

1. 利用乘法公式计算正确的是（　　）

A、 ${(4 x - 3)}^{2} = 8 x^{2} + 12 x - 9$ B、 $(2 m + 5) (2 m - 5) = 4 m^{2} - 5$ C、 $(a + b) (a + b) = a^{2} + b^{2}$ D、 ${(4 x + 1)}^{2} = 16 x^{2} + 8 x + 1$

查看试题解析
2. 如果 $x^{2} + y^{2} = 8 ， x + y = 3$ ，则 $x y =$ （）

A、1 B、 $\frac{1}{2}$ C、2 D、 $- \frac{1}{2}$

查看试题解析
3. 如图所示，将如图一所示的大小相同的四个小正方形按图二所示的方式放置在一个边长为a的大正方形中，中间恰好空出两条互相垂直的宽都为b的长方形，根据图二中阴影部分的面积计算方法可以验证的公式为（）

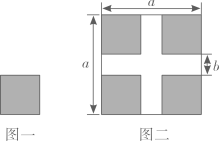A、（a+b）（a﹣b）＝a²﹣b² B、（a+b）²＝a²+2ab+b² C、（a﹣b）²＝a²﹣2ab+b² D、（a﹣b）²＝（a+b）²﹣4ab

查看试题解析
4. 若 $a + \frac{1}{a} = 3$ ，则 $\frac{a^{2}}{a^{4} + a^{2} + 1}$ 的值是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{5}$ C、 $\frac{1}{8}$ D、 $\frac{1}{9}$

查看试题解析
5. 已知 $x$ 为任意实数，则多项式 $x - 1 - \frac{1}{4} x^{2}$ 的值为（）

A、一定为负数 B、不可能为正数 C、一定为正数 D、正数或负数或零

查看试题解析
6. 已知一个正方形的边长为a＋1，则该正方形的面积为（）

A、a²＋2a＋1 B、a²－2a＋1 C、a²＋1 D、4a＋4

查看试题解析
7. 若 $x + y = 6$ ， $x^{2} + y^{2} = 20$ ，求 $x y$ 的值是（）

A、6 B、8 C、26 D、20

查看试题解析
8. 已知 $\frac{1}{4} m^{2} + \frac{1}{4} n^{2} = n - m - 2$ ，则 $\frac{1}{m} - \frac{1}{n}$ 的值等于（）

A、1 B、0 C、 $- 1$ D、 $- \frac{1}{4}$

查看试题解析
9. 由图你能根据面积关系得到的数学公式是（）

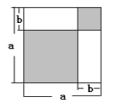A、a²－b²＝（a＋b）（a－b） B、（a＋b）²＝a²＋2ab＋b² C、（a－b）²＝a²－2ab＋b² D、a（a＋b）＝a²＋ab

查看试题解析
10. 如图，根据计算正方形ABCD的面积，可以说明下列哪个等式成立（）

A、（a﹣b）²=a²﹣2ab+b² B、（a+b）²=a²+2ab+b² C、（a+b）（a﹣b）=a²﹣b² D、a（a﹣b）=a²﹣ab

查看试题解析

二、填空题

11. 已知 $x - \frac{1}{x} = 4$ ，则 $x^{2} + \frac{1}{x^{2}} =$ .

查看试题解析
12. 已知 $x - y = 2$ ， $x y = - 1$ ，则 $x^{2} + y^{2} =$ .

查看试题解析
13. 已知a-b=3，ab=2则a²+b²的值为.

查看试题解析
14. 已知 $4 y^{2} - m y + 9$ 是完全平方式，则m的值为．

查看试题解析
15. 若a+b=8，ab=-5，则 ${(a - b)}^{2}$ ＝

查看试题解析

三、解答题

16. 已知A，B，C为△ABC的三边，且a²+b²+b²=ab+bc+ac，试判断△ABC的形状，并说明理由

查看试题解析
17. 已知m²＋ $\frac{1}{m^{2}}$ ＝4，求m＋ $\frac{1}{m}$ 和m－ $\frac{1}{m}$ 的值．

查看试题解析
18. $a + b = 5 ， a b = - 2 ，$ 求 $a^{2} + b^{2}$ 和 $（ a - b ）^{2}$ 的值.

查看试题解析
19. 已知 ${(m + n)}^{2} = 9, {(m - n)}^{2} = 1$ ，求 $m^{2} + n^{2} + m n$ 的值.

查看试题解析
20. 已知a，b，c是 $△ A B C$ 的三边长，且满足 $a^{2} + b^{2} - 4 a - 8 b + 20$ ＝ $0$ ， $c$ ＝ $3 c m$ ，求 $△ A B C$ 的周长．

查看试题解析
21. 已知 ${(a + b)}^{2} = 60$ ， ${(a - b)}^{2} = 80$ ，求 $a^{2} + b^{2}$ 及 $a b$ 的值．

查看试题解析
22. 已知a，b，c是△ABC的三边长，且满足a²+b²﹣4a﹣8b+20=0，c=3cm，求△ABC的周长.

查看试题解析
23. 数学课上老师出了一道题：计算296²的值，喜欢数学的小亮举手做出这道题，他的解题过程如下：
296²=(300－4)²=300²－2×300×(－4)+4²

=90000+2400+16=92416

老师表扬小亮积极发言的同时，也指出了解题中的不符合题意，你认为小亮的解题过程错在哪儿，并给出正确的答案.

查看试题解析
24. 用若干个形状、大小完全相同的矩形纸片围成正方形，4个矩形纸片围成如
图①所示的正方形，其阴影部分的面积为12；8个矩形纸片围成如图②所示的正方形，其阴影部分的面积为8；12个矩形纸片围成如图③所示的正方形，请求出其阴影部分的面积为多少．

查看试题解析

（人教版）2022-2023学年度第一学期八年级数学14.2.2 完全平方公式 同步测试

一、单选题

二、填空题

三、解答题

（人教版）2022-2023学年度第一学期八年级数学14.2.2 完全平方公式同步测试