浙江省金华市金东区2021-2022学年八年级下学期期末检测数学试题
试卷更新日期:2022-07-19 类型:期末考试
一、选择题(本大题共有10小题,每小题3分,共30分,)
-
1. 要使二次根式 有意义,则x的取值范围是( )A、x>﹣2 B、x≥﹣2 C、x≠﹣2 D、x≤﹣22. 下列方程有两个相等的实数根的是( )A、x2+5x﹣6=0 B、x2﹣5x+6=0 C、x2﹣6x+9=0 D、x2+6x﹣9=03. “科学用眼,保护视力”是青少年珍爱生命的表现,某班50名同学的视力数据如表.则视力的众数是( )
视力
4.3
4.4
4.5
4.6
4.7
4.8
4.9
5.0
人数
2
3
6
9
12
10
5
3
A、4.5 B、4.6 C、4.7 D、4.84. 二次函数y=2(x+1)2+3的顶点坐标是( )A、(﹣1,﹣3) B、(﹣1,3) C、(1,﹣3) D、(1,3)5. 如图添加下列一个条件,能使平行四边形ABCD成为菱形的是( )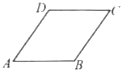 A、AB=CD B、AC=BD C、∠BAD=90° D、AB=BC6. 某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,设每次降价的百分率为x,则下面所列的方程中正确的是( )A、560(1﹣x)2=315 B、560(1+x)2=315 C、560(1﹣2x)2=315 D、560(1﹣x2)=3157. 如图,矩形ABCD的对角线AC,BD交于点O,点E,F分别为AO,AD的中点,若EF=4,AB=8,则∠ACB的度数为( )
A、AB=CD B、AC=BD C、∠BAD=90° D、AB=BC6. 某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,设每次降价的百分率为x,则下面所列的方程中正确的是( )A、560(1﹣x)2=315 B、560(1+x)2=315 C、560(1﹣2x)2=315 D、560(1﹣x2)=3157. 如图,矩形ABCD的对角线AC,BD交于点O,点E,F分别为AO,AD的中点,若EF=4,AB=8,则∠ACB的度数为( ) A、30° B、35° C、45° D、60°8. 若点A(a﹣1,y1),B(a+1,y2)是反比例函数y=﹣ 图象的两个点,且y1<y2 , 则a的取值范围是( )A、a<﹣1 B、﹣1<a<1 C、a>1 D、a<﹣1或a>19. 若p,q是一元二次方程x2+3x﹣9=0的两个根,则p2+2p﹣q的值是( )A、6 B、9 C、12 D、1310. 如图,在矩形ABCO中,点D在BC边上,连结AD,把△ABD沿AD折叠,使点B恰好落在OC边上的点E处,已知B(10,8),反比例函数y= (k≠0)的图象经过点D,则k的值为( )
A、30° B、35° C、45° D、60°8. 若点A(a﹣1,y1),B(a+1,y2)是反比例函数y=﹣ 图象的两个点,且y1<y2 , 则a的取值范围是( )A、a<﹣1 B、﹣1<a<1 C、a>1 D、a<﹣1或a>19. 若p,q是一元二次方程x2+3x﹣9=0的两个根,则p2+2p﹣q的值是( )A、6 B、9 C、12 D、1310. 如图,在矩形ABCO中,点D在BC边上,连结AD,把△ABD沿AD折叠,使点B恰好落在OC边上的点E处,已知B(10,8),反比例函数y= (k≠0)的图象经过点D,则k的值为( ) A、20 B、30 C、40 D、48
A、20 B、30 C、40 D、48二、填空题(本大题共有6小题,每小题4分,共24分)
-
11. 化简(﹣ )2的结果是 .12. 数据1,2,2,2,3的方差是 .13. 如果一个多边形的内角和等于其外角和的两倍,那么这个多边形是边形.14. 若m是方程2x2﹣3x﹣1=0的一个根,则6m2﹣9m+1的值为 .15. 已知二次函数y=x2﹣2x﹣3,当y≥5时,自变量x的取值范围是 .16. 如图,矩形ABCD中,点E,F,G分别在CD,AD,BC边上,CE=2,DE=1,BE平分∠FBC,∠BEF=∠BEG=45°,则线段DF的长为 , 线段BC的长为 .

三、解答题(本大题共有8小题,共66分)
-
17. 计算:(1)、 × ;(2)、 .18. 解方程:(1)、x2﹣2x﹣3=0;(2)、(2x+1)2=(x﹣1)2 .19. 尊老爱幼是中华民族的传统美德,某商店为老人推出一款特价商品,每件商品的进价为15元,促销前销售单价为25元,平均每天能售出80件;根据市场调查,销售单价每降低0.5元,平均每天可多售出20件.不考虑其他因素的影响,若商店销售这款商品的利润要达到平均每天1280元,销售单价应降低多少元?20. 已知点E,F分别是▱ABCD的边BC,AD的中点,连结AC,AE,CF.
 (1)、求证:四边形AECF是平行四边形;(2)、若BC=12,∠BAC=90°,求▱AECF的周长.21. 甲、乙两位同学参加数学综合素质测试,各项成绩如表(单位:分)
(1)、求证:四边形AECF是平行四边形;(2)、若BC=12,∠BAC=90°,求▱AECF的周长.21. 甲、乙两位同学参加数学综合素质测试,各项成绩如表(单位:分)数与代数
空间与图形
统计与概率
综合与实践
学生甲
90
93
89
90
学生乙
94
92
94
86
(1)、分别求学生甲、乙成绩的中位数.(2)、如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:2:2:3计算,那么甲、乙的数学综合素质成绩谁更好?22. 如图,正方形ABCD,边长为2,点E,F分别是AB,CD的中点,连结CE,AF,过点D作DG⊥AF,垂足为G,延长DG交CE于点H. (1)、求DG的长.(2)、求GH的长.(3)、求EH的长.23. 如图,直线y=x﹣3交x轴于点B,交y轴于点A,抛物线y=ax2+4x+c经过点A,B,顶点为点C.
(1)、求DG的长.(2)、求GH的长.(3)、求EH的长.23. 如图,直线y=x﹣3交x轴于点B,交y轴于点A,抛物线y=ax2+4x+c经过点A,B,顶点为点C.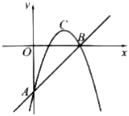 (1)、求抛物线的解析式及点C的坐标.(2)、将抛物线y=ax2+4x+c向下平移m个单位长度,点C的对应点为D,连结AD,BD,若S△ABD=2,求m的值.24. 如图,在平面直角坐标系中,点B在第一象限,BA⊥x轴于A,BC⊥y轴于C,BA=3,BC=5,有一反比例函数图象刚好过点B.
(1)、求抛物线的解析式及点C的坐标.(2)、将抛物线y=ax2+4x+c向下平移m个单位长度,点C的对应点为D,连结AD,BD,若S△ABD=2,求m的值.24. 如图,在平面直角坐标系中,点B在第一象限,BA⊥x轴于A,BC⊥y轴于C,BA=3,BC=5,有一反比例函数图象刚好过点B.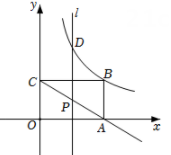 (1)、分别求出过点B的反比例函数和过A,C两点的一次函数的表达式.(2)、动点P在射线CA(不包括C点)上,过点P作直线l⊥x轴,交反比例函数图象于点D.是否存在这样的点Q,使得以点B,D,P,Q为顶点的四边形为菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
(1)、分别求出过点B的反比例函数和过A,C两点的一次函数的表达式.(2)、动点P在射线CA(不包括C点)上,过点P作直线l⊥x轴,交反比例函数图象于点D.是否存在这样的点Q,使得以点B,D,P,Q为顶点的四边形为菱形?若存在,求出点Q的坐标;若不存在,请说明理由.