浙江省金华市东阳市2021-2022学年七年级下学期期末数学试卷

试卷更新日期：2022-07-19 类型：期末考试

进入出卷网下载

一、精心选一选：（本题共30分，每小题3分）

1. 如图，AB、CD被EF所截，则∠1与∠2是一对（）

A、同位角 B、内错角 C、同旁内角 D、都不是

查看试题解析
2. 目前代表华为手机最强芯片的膜麟990处理器采用0.0000007cm工艺制程，数0.0000007用科学记数法表示为（）

A、7×10^﹣⁶ B、7×10^﹣⁷ C、0.7×10^﹣⁶ D、0.7×10^﹣⁷

查看试题解析
3. 为了调查某校学生的身高情况，在全校的900名学生中随机抽取了80名学生，下列说法正确的是（）

A、此次调查属于全面调查 B、样本容量是80 C、900名学生是总体 D、被抽取的每一名学生称为个体

查看试题解析
4. 直径为4cm的圆O₁平移5cm到圆O₂ ，则图中阴影部分的面积为（）

A、2π B、10 C、4π D、20

查看试题解析
5. 若a^x＝3，a^y＝2，则a^y^﹣^x等于（）

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、L D、6

查看试题解析
6. 如图，一块含60°角的直角三角板放置在两条平行线上，若∠1＝43°，则∠2为（）

A、17° B、27° C、37° D、47°

查看试题解析
7. 使（x²+px+8）（x²﹣3x+q）的积中不含x²和x³的p、q的值分别是（）

A、p＝0，q＝0 B、p＝﹣3，q＝﹣9 C、p＝﹣3，q＝1 D、p＝3，q＝1

查看试题解析
8. 若关于x的方程 $\frac{x}{x - 3} + \frac{3 a}{3 - x} =$ 3a有增根，则a的值为（）

A、﹣l B、 $\frac{1}{7}$ C、 $\frac{1}{3}$ D、1

查看试题解析
9. 设a＝19²×918，b＝888²﹣30² ， c＝1053²﹣747² ，则数a，b，c按从小到大的顺序排列，正确的是（）

A、a＜c＜b B、a＜b＜c C、b＜a＜c D、b＜c＜a

查看试题解析
10. 《九章算术》是人类科学史上应用数学的“算径之首“，书中记载：今有三人共车，二车空；二人共车，九人步.问：人与车各几何？译文：若3人坐一辆车，则两辆车是空；若2人坐一辆车，则9人需要步行；问：人与车各多少？设x辆车，人数为y人，根据题意可列方程组为（）

A、 ${\begin{array}{l} y = 3 x - 2 \\ y = 2 x + 9 \end{array}$ B、 ${\begin{array}{l} y = 3 x - 2 \\ y = 2 x - 9 \end{array}$ C、 ${\begin{array}{l} y = 3 (x - 2) \\ y = 2 x + 9 \end{array}$ D、 ${\begin{array}{l} y = 3 (x - 2) \\ y = 2 x - 9 \end{array}$

查看试题解析

二、用心填一填（本题共24分，每小题4分）

11. 若使分式 $\frac{x}{x - 3}$ 有意义的取值范围是 .

查看试题解析
12. 计算：2022⁰﹣（ $\frac{1}{2}$ ）^﹣¹＝.

查看试题解析
13. 一次数学测试后，某班50名的成绩被分为5组，若第1﹣4组的频数分别为12、10、15、x，第5组是的频率是0.1，则x值为 .

查看试题解析
14. 如图，木棒AB、CD与EF分别在G、H处可旋转的螺丝铆住，∠EGB＝100°，∠EHD＝80°，将木棒AB绕点G旋转到与木棒CD平行，则至少要旋转度.

查看试题解析
15. 小聪解方程组 ${\begin{array}{l} 2 x + y = � \\ 2 x - y = 12 \end{array}$ 的解为 ${\begin{array}{l} x = 5 \\ y = � \end{array}$ ，由于不小心，滴上了两滴墨水，刚好遮住了两个数，请你帮他找回，前后两个数分别是、.

查看试题解析
16. 在学完书中例题后，小聪想用现有的硬纸板裁成如图①的长方形和正方形作为侧面与底面，做成如图②的竖式和横式两种无盖纸盒.已知一张硬纸板的裁剪方式有两种（均有余料）），方式一：裁成3个长方形与一个正方形：方式二：裁成2个长方形与2个正方形.现小聪将m张硬纸板用方式一裁剪，n张硬纸板用方式二裁剪，则：

(1)、两种方式共裁出长方形张，正方形张（用m、n的代数式表示）；

(2)、当10＜m＜15时，所裁得的长方形与正方形纸板恰好用完，做成的两种无盖纸盒一共可能是个.

查看试题解析

三、细心答一答（本题共66分）

17. 计算：

(1)、（﹣x²y⁵）•（xy）³；

(2)、（a²﹣b²）²+2a（ab﹣1）.

查看试题解析
18. 解方程组：

(1)、 ${\begin{array}{l} 3 x - 4 (x - y) = 3 \\ x - y = 3 \end{array}$ ；

(2)、 $\frac{1}{x} + \frac{5 x}{x - 3} = 5$ .

查看试题解析
19. 如图，已知DE⊥AC于点E，BC⊥AC于点C，FG⊥AB于点G，∠1＝∠2，求证：CD⊥AB.
证明：

∵DE⊥AC，BC⊥AC（已知）；

∴DE∥      ▲      （）；

∴∠2＝      ▲      （两直线平行，内错角相等）；

∵∠1＝∠2（已知）；

∴∠1＝      ▲      （）；

∴GF∥CD（）；

∵FG⊥AB（已知）

∴CD⊥AB.

查看试题解析
20.

(1)、先化简，再求值： $\frac{a + b}{a b} \div (\frac{a}{b} - \frac{b}{a})$ ，其中a $= \frac{1}{3}$ ， b $= \frac{1}{2}$ .

(2)、已知xy＝﹣3，x﹣2y $= \frac{1}{3}$ ，求﹣x⁴y²+4x³y³﹣4x²y⁴的值.

查看试题解析
21. 某校学生参加防疫知识竞赛，从中抽取了部分学生成绩（成绩为整数，且满分为100分）进行统计，绘制如下不完整的频数分布直方图，若将频数分布直方图划分的五组从左至右依次记为 A，B，C，D、E，绘制成扇形统计图，其中A组的频数比B组小24，请你根据信息回答：

(1)、D组的边界值为、；

(2)、求a、b、n的值，并补全频数直图；

(3)、若成绩在80分以上为优秀，全校共有1000名学生，估计成绩优秀的学生有多少名？

查看试题解析
22. 某运输公司现有190吨防疫物资需要运往外地，拟安排A、B两种货车将全部货物一次运完（两种货车均满载），已知A、B两种货车近期的三次运输记录，如下表：

A货车（辆）
B货车（辆）
防疫物资（吨）
第一次
12
8
360
第二次
18
12
▇
第三次
5
4
160

(1)、表格中被污渍盖住的数是；

(2)、请问A、B两种货车每辆每次分别可以运送防疫物资多少吨？

(3)、请你通过计算说明所有可行的运输方案.

查看试题解析
23. 教材中的探究：通过用不同的方法计算同一图形面积，得到相应的等式，从而探求出多项式乘法或分解因式的新途径.例如，选取图①中的正方形、长方形硬纸片共6块，拼出一个如图②的长方形，计算它的面积写出相应的等式：a²+3ab+2b²＝（a+2b）（a+b）或（a+2b）（a+b）＝a²+3ab+2b².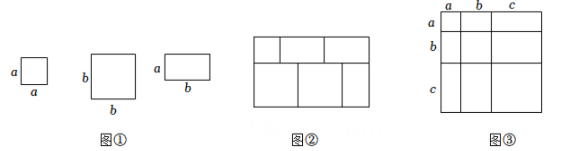

(1)、请根据图③写出代数恒等式，并根据所写恒等式计算（x﹣2y﹣3）²；

(2)、若x²+y²+z²＝1，xy+yz+xz＝3，求x+y+z的值.

(3)、试借助图①的硬纸片，利用拼图的方法把二次三项式3a²+7ab+2b²分解因式，并把所拼的图形画在虚线方框内.

查看试题解析
24. 如图，AB、CD被AC所截，AB∥CD，∠CAB＝108°，点P为直线AB上一动点（不与点A重合），连CP，作∠ACP和∠DCP的平分线分别交直线AB于点E、F.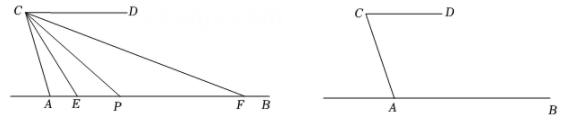

(1)、当点P在点A的右侧时；
①若∠ACP＝36°，则此时CP是否平分∠ECF，请说明理由.
②求∠ECF的度数.

(2)、在点P运动过程中，直接写出∠APC与∠AFC之间的数量关系.

查看试题解析

	A货车（辆）	B货车（辆）	防疫物资（吨）
第一次	12	8	360
第二次	18	12	▇
第三次	5	4	160