浙江省宁波市奉化区等三县2021-2022学年七年级下学期期末数学试卷

试卷更新日期：2022-07-19 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，共30分）

1. “冰墩墩”是第二十四届冬季奥林匹克运动会的吉祥物，如图，通过平移“冰墩墩”可以得到的图形是（）

A、 B、 C、 D、

查看试题解析
2. 下列调查中，适合采用抽样调查的是（）

A、了解全班学生的身高 B、调查某品牌电视机的使用寿命 C、对乘坐高铁的乘客进行安检 D、检测“神舟十三号”各零部件的质量情况

查看试题解析
3. 预防新冠病毒用肥皂勤洗手，肥皂泡的厚度约为0.0000006米，用科学记数法表示0.0000006为（）

A、 $6 \times 1 0^{- 7}$ B、 $0.6 \times 1 0^{- 7}$ C、 $6 \times 1 0^{- 6}$ D、 $0.6 \times 1 0^{- 6}$

查看试题解析
4. 下列运算正确的是（）

A、 $(a^{2})^{3} = a^{5}$ B、 $(a b)^{3} = a^{3} b^{3}$ C、 $a^{2} \cdot a^{3} = a^{6}$ D、 $a^{2} \div a = a^{2}$

查看试题解析
5. 下列添括号正确的是（）

A、 $- b - c = - (b - c)$ B、 $- 2 x + 6 y = - 2 (x - 6 y)$ C、 $a - b = + (a - b)$ D、 $x - y - 1 = x - (y - 1)$

查看试题解析
6. 下列各式从左向右的变形中，是因式分解的为（）

A、 $(x - 1) (x + 1) = x^{2} - 1$ B、 $x (x + 1) = x^{2} + x$ C、 $3 x^{2} - 3 x + 1 = 3 x (x - 1) + 1$ D、 $a^{2} + 2 a b + b^{2} = (a + b)^{2}$

查看试题解析
7. 若方程组 ${\begin{array}{l} 2 x + y = m \\ 2 x - y = 10 \end{array}$ 的解为 ${\begin{array}{l} x = 4 \\ y = n \end{array}$ ，小亮求解时不小心滴上了两滴墨水，刚好遮住了 $m$ 和 $n$ 两数，则这两数分别为（）

A、6和-2 B、10和2 C、-6和4 D、4和6

查看试题解析
8. 若将分式 $\frac{x - y}{2 x y}$ 中的 $x$ 和 $y$ 都扩大到原来的10倍，则分式的值（）

A、缩小到原来的 $\frac{1}{10}$ B、不变 C、扩大到原来的10倍 D、缩小到原来的 $\frac{1}{100}$

查看试题解析
9. 如图，直线 $a / / b$ ，一块含 $45 °$ 角的直角三角板的直角顶点恰好在直线 $a$ 上，若 $∠ 1 = 30 °$ ，则 $∠ 2$ 的度数是（）

A、 $55 °$ B、 $65 °$ C、 $75 °$ D、 $80 °$

查看试题解析
10. 如图，将两张长为 $a$ ，宽为 $b$ 的长方形纸片按图1，图2两种方式放置，图1和图2中两张长方形纸片重叠部分分别记为①和②，正方形 $A B C D$ 中未被这两张长方形纸片覆盖部分用阴影表示，图1和图2中阴影部分的面积分别记为 $S_{1}$ 和 $S_{2} .$ 若知道下列条件，仍不能求 $S_{1} - S_{2}$ 值的是（）

A、长方形纸片长和宽的差 B、长方形纸片的周长和面积 C、①和②的面积差 D、长方形纸片和①的面积差

查看试题解析

二、填空题（本大题共6小题，共24分）

11. 若分式 $\frac{m}{m - 2}$ 有意义，则 $m$ 的取值范围是.

查看试题解析
12. 计算 $8 x^{2} y^{4} \div (4 x y^{2}) =$ .

查看试题解析
13. 已知一个样本有40个数据，把它分成5组，第一组到第四组的频数分别是10、4、 $x$ 、 $16$ ，第五组的频率是0.1，则 $x$ 的值为.

查看试题解析
14. 若 $x - y = 3$ ， $x y = 1$ ，则 $x^{2} + y^{2} =$ .

查看试题解析
15. 关于 $x$ 的分式方程 $\frac{k - 1}{x^{2} - 1} - \frac{1}{x - 1} = \frac{k}{x + 1}$ 有增根，则 $k =$ .

查看试题解析
16. 阅读材料：若 $x^{3} + 2 x^{2} - 2 x + m (m$ 为常数 $)$ 有一个因式为 $(x - 1)$ ，则如何因式分解 $x^{3} + 2 x^{2} - 2 x + m$ ？
解：因为 $x^{3} + 2 x^{2} - 2 x + m$ 有一个因式为 $(x - 1)$ ，所以当 $x - 1 = 0$ 时， $x^{3} + 2 x^{2} - 2 x + m = 0$ ，于是把 $x = 1$ 代入 $x^{3} + 2 x^{2} - 2 x + m = 0$ 得 $1 + 2 - 2 + m = 0$ ，解得 $m = - 1$ ，原代数式变为 $x^{3} + 2 x^{2} - 2 x - 1$ ，接着可以通过列竖式做多项式除法的方式求出其它因式，如图所示，则因式分解 $x^{3} + 2 x^{2} - 2 x - 1 = (x - 1) (x^{2} + 3 x + 1)$

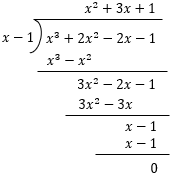
若 $x^{3} + 4 x^{2} + m x + 2 (m$ 为常数 $)$ 有一个因式为 $(x + 2)$ ，则因式分解 $x^{3} + 4 x^{2} + m x + 2 =$ .

查看试题解析

三、解答题（本大题共8小题，共66分）

17. 计算：

(1)、 $(- 1)^{2} + (\frac{1}{2})^{- 3} - 202 2^{0}$ ；

(2)、 $(m + 2)^{2} - (m + 1) (m - 1) - 4 (m + 2)$ .

查看试题解析
18. 因式分解：

(1)、 $m^{3} n - 9 m n$ ；

(2)、 $(x^{2} + y^{2})^{2} - 4 x^{2} y^{2}$ .

查看试题解析
19. 解方程.

(1)、 ${\begin{array}{l} x + 2 y = 15 \\ x - 3 y = 5 \end{array}$ ；

(2)、 $\frac{2}{x^{2} - x} + 1 = \frac{x}{x - 1}$ .

查看试题解析
20. 先化简，再求值： $(1 - \frac{3}{x + 2}) \div \frac{x^{2} - 1}{2 x + 4}$ ，其中 $x = 3$ .

查看试题解析
21. 某校组织开展了丰富多彩的主题活动，设置了“ $A$ ：诗歌朗诵表演， $B$ ：歌舞表演， $C$ ：书画作品展览， $D$ ：手工作品展览”四个专项，每个学生只能报名参加其中一个专项.为了解活动开展情况，学校随机抽取了部分学生进行调查，绘制了如图所示的不完整的条形统计图和扇形统计图.

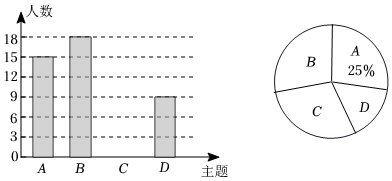(1)、本次随机调查的学生人数是人.

(2)、请你补全条形统计图.

(3)、在扇形统计图中，“ $B$ ”所在扇形的圆心角为度.

(4)、若该校有学生1800人，则全校选择D：手工作品展览的学生约有多少人？

查看试题解析
22. 已知：如图， $∠ E A C = ∠ C$ ， $∠ E = ∠ B$ .

(1)、证明 $A B / / D E$ .

(2)、若 $A B ⊥ A C$ 于点 $A$ ， $∠ E A C = 30 °$ ，求 $∠ E D B$ 的度数.

查看试题解析
23. 为开展“光盘行动”，某学校食堂规定：每天午餐“光盘”的学生，餐后可获得奖品香蕉和橘子.两天时间里，学校食堂采购奖品香蕉和橘子分别花费了400元和600元，已知这两天食堂所采购的香蕉比橘子少10千克，香蕉单价是橘子单价的80%.

(1)、橘子和香蕉的单价分别是每千克多少元？

(2)、若每千克香蕉有8根，每千克橘子有10只，且第一天每人可获得1根香蕉和3只橘子，第二天每人可获得2根香蕉和2只橘子，则这两天分别有多少学生获得奖品？

查看试题解析
24. 我们把形如 $x + \frac{a b}{x} = a + b (a ， b$ 不为零 $)$ ，且两个解分别为 $x_{1} = a$ ， $x_{2} = b$ 的方程称为“十字分式方程”.
例如 $x + \frac{3}{x} = 4$ 为十字分式方程，可化为 $x + \frac{1 \times 3}{x} = 1 + 3$ ， $∴ x_{1} = 1$ ， $x_{2} = 3$ .

再如 $x + \frac{8}{x} = - 6$ 为十字分式方程，可化为 $x + \frac{(- 2) \times (- 4)}{x} = (- 2) + (- 4)$ ， $∴ x_{1} = - 2$ ， $x_{2} = - 4$ .

应用上面的结论解答下列问题：

(1)、若 $x + \frac{6}{x} = - 5$ 为十字分式方程，则 $x_{1} =$ ， $x_{2} =$ .

(2)、若十字分式方程 $x - \frac{5}{x} = - 2$ 的两个解分别为 $x_{1} = m$ ， $x_{2} = n$ ，求 $\frac{n}{m} + \frac{m}{n}$ 的值.

(3)、若关于 $x$ 的十字分式方程 $x - \frac{2 k^{2} + 3 k}{x - 2} = - k - 1$ 的两个解分别为 $x_{1}$ ， $x_{2} (k > 0 ， x_{1} > x_{2})$ ，求 $\frac{x_{1} - 2}{x_{2} + 1}$ 的值.

查看试题解析