重庆市綦江区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-19 类型:期末考试
一、单选题
-
1. 下列各图给出了变量x与y之间的对应关系,其中y是x的函数的是( )A、
 B、
B、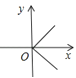 C、
C、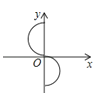 D、
D、 2. 准备在甲,乙,丙,丁四人中选取成绩稳定的一名参加射击比赛,在相同条件下每人射击10次,已知他们的平均成绩相同,方差分别是 , , , , 则应该选择哪位运动员参赛( )A、甲 B、乙 C、丙 D、丁3. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、4. 勾股定理是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中不能证明勾股定理的是( )A、
2. 准备在甲,乙,丙,丁四人中选取成绩稳定的一名参加射击比赛,在相同条件下每人射击10次,已知他们的平均成绩相同,方差分别是 , , , , 则应该选择哪位运动员参赛( )A、甲 B、乙 C、丙 D、丁3. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、4. 勾股定理是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中不能证明勾股定理的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,在菱形中,对角线 , 相交于点 , 是的中点,连接 , 若 , 则的长是( )
5. 如图,在菱形中,对角线 , 相交于点 , 是的中点,连接 , 若 , 则的长是( ) A、9 B、8 C、7 D、66. 已知点 , , 都在直线上,则 , , 的值的大小关系是( )A、 B、 C、 D、7. 估计-2的值在( )A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间8. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别是3、6、2、3,则最大正方形的面积是( )
A、9 B、8 C、7 D、66. 已知点 , , 都在直线上,则 , , 的值的大小关系是( )A、 B、 C、 D、7. 估计-2的值在( )A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间8. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别是3、6、2、3,则最大正方形的面积是( ) A、14 B、34 C、58 D、729. 某校6名学生在2020年中考中的体育成绩(满分50分)统计如图所示,则这组数据的众数、中位数分别是( )
A、14 B、34 C、58 D、729. 某校6名学生在2020年中考中的体育成绩(满分50分)统计如图所示,则这组数据的众数、中位数分别是( ) A、50,48 B、48,49 C、50,49 D、48,4810. 下列说法中不正确的是( )A、对角线垂直的平行四边形是菱形 B、对角线相等的平行四边形是矩形 C、对角线互相垂直平分的四边形是正方形 D、菱形的面积等于对角线乘积的一半11. 如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE和等边△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF、EF,则以下四个结论,正确的是( )
A、50,48 B、48,49 C、50,49 D、48,4810. 下列说法中不正确的是( )A、对角线垂直的平行四边形是菱形 B、对角线相等的平行四边形是矩形 C、对角线互相垂直平分的四边形是正方形 D、菱形的面积等于对角线乘积的一半11. 如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE和等边△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF、EF,则以下四个结论,正确的是( )①△CDF≌△EBC;②∠CDF=∠EAF;③CG⊥AE;④△CEF是等边三角形.
 A、③④ B、①②④ C、①②③ D、①②③④12. 若关于的一元一次不等式组恰有4个整数解,且一次函数不经过第三象限,则所有满足条件的整数的值之和是( )A、-7 B、-12 C、-9 D、-11
A、③④ B、①②④ C、①②③ D、①②③④12. 若关于的一元一次不等式组恰有4个整数解,且一次函数不经过第三象限,则所有满足条件的整数的值之和是( )A、-7 B、-12 C、-9 D、-11二、填空题
-
13. 如图,两个正方形边长分别为、 , 图中阴影部分的面积为.
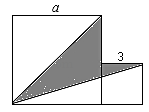 14. 实数 , 在数轴上对应点的位置如图所示,化简的结果是.
14. 实数 , 在数轴上对应点的位置如图所示,化简的结果是.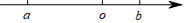 15. 小南骑自行车从地向地出发,1小时后小通步行从地向地出发.如图,两条线段、分别表示小南、小通离地的距离y(单位:km)与所用时间x(单位:h)之间的函数图象,根据图中的信息,则小南、小通的速度分别是 km/ h, km/ h.
15. 小南骑自行车从地向地出发,1小时后小通步行从地向地出发.如图,两条线段、分别表示小南、小通离地的距离y(单位:km)与所用时间x(单位:h)之间的函数图象,根据图中的信息,则小南、小通的速度分别是 km/ h, km/ h. 16. 重庆某大学对重庆某村实施“技术助农”.该村种植有A、B、C三种经济作物,助农前,A,B,C三种作物亩数比例为2:5:3;助农后,三种经济作物的亩数都得以增加,其中B作物增加的亩数占总增加亩数的.助农前,C作物的亩产量是B作物亩产量的2.5倍,A,B两种作物的亩产量之和恰好是C作物的亩产量;助农后,A,B两种作物的亩产量分别增加了和 , A,B两种作物的亩产量之和恰好仍是C作物的亩产量.若助农后,B作物的产量比助农前A,B产量之和多 , 而C作物的产量比助农前A,B,C三种作物产量的总和还多5%,则助农前后A作物的产量之比为.
16. 重庆某大学对重庆某村实施“技术助农”.该村种植有A、B、C三种经济作物,助农前,A,B,C三种作物亩数比例为2:5:3;助农后,三种经济作物的亩数都得以增加,其中B作物增加的亩数占总增加亩数的.助农前,C作物的亩产量是B作物亩产量的2.5倍,A,B两种作物的亩产量之和恰好是C作物的亩产量;助农后,A,B两种作物的亩产量分别增加了和 , A,B两种作物的亩产量之和恰好仍是C作物的亩产量.若助农后,B作物的产量比助农前A,B产量之和多 , 而C作物的产量比助农前A,B,C三种作物产量的总和还多5%,则助农前后A作物的产量之比为.三、解答题
-
17. 计算:(1)、(2)、18. 已知,如图,BD是菱形ABCD的对角线,∠CBD=76°.
 (1)、请用尺规作图法作线段AB的垂直平分线EF,垂足为点E,交AD于点F,连接BF;(不写作法,保留作图痕迹)(2)、在(1)的条件下,求∠DBF的度数.19. 一个有进水管与出水管的容器,从某时刻开始3min内只进水不出水,在随后的9min内既进水又出水,每分种的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间(单位:min)之间的关系如图所示.
(1)、请用尺规作图法作线段AB的垂直平分线EF,垂足为点E,交AD于点F,连接BF;(不写作法,保留作图痕迹)(2)、在(1)的条件下,求∠DBF的度数.19. 一个有进水管与出水管的容器,从某时刻开始3min内只进水不出水,在随后的9min内既进水又出水,每分种的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间(单位:min)之间的关系如图所示.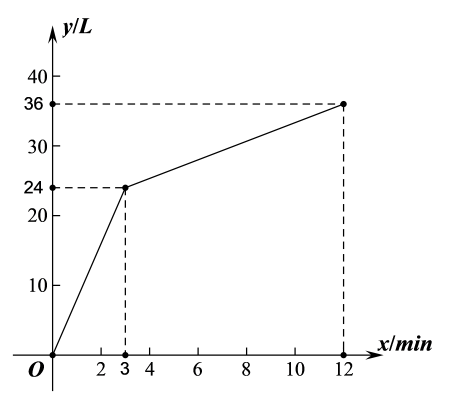 (1)、当0≤x≤3时,求y关于x的函数解析式;(2)、当3< x≤12时,求y关于x的函数解析式;(3)、求进水速度是出水速度的多少倍?20. 为进一步推动各级各类学校新型冠状病毒肺炎疫情防控工作,向广大教职工和学生普及新型冠状病毒肺炎疫情防控知识,市教育厅要求各级各类学校认真学习相关资料.某中学为了解学生的学习成果,对学生进行了新型冠状病毒肺炎防控知识测试,德育处随机从七八两个年级各抽取20名学生的答卷成绩(单位:分)进行统计分析,过程如下:
(1)、当0≤x≤3时,求y关于x的函数解析式;(2)、当3< x≤12时,求y关于x的函数解析式;(3)、求进水速度是出水速度的多少倍?20. 为进一步推动各级各类学校新型冠状病毒肺炎疫情防控工作,向广大教职工和学生普及新型冠状病毒肺炎疫情防控知识,市教育厅要求各级各类学校认真学习相关资料.某中学为了解学生的学习成果,对学生进行了新型冠状病毒肺炎防控知识测试,德育处随机从七八两个年级各抽取20名学生的答卷成绩(单位:分)进行统计分析,过程如下:收集数据
八年级:
85
80
95
100
90
95
85
65
75
85
95
90
70
90
100
80
80
90
90
75
七年级:
70
70
80
95
70
100
90
75
80
70
95
100
80
80
100
80
95
100
95
90
整理数据

八年级
2
5
8
5
七年级
4
6
2
8
分析数据
统计量
平均数(分)
中位数(分)
众数(分)
八年级
85.75
87.5
七年级
85.75
80
应用数据
(1)、填空:(分),(分);(2)、在这次测试中,八年级学生甲与七年级学生乙的成绩都是86分,请判断两人在各自年级的排名谁更靠前,并说明理由.(3)、看完统计数据,你认为对新型冠状病毒肺炎防护知识掌握更好的是哪个年级?并说明理由.21. 如图,有人在岸上点的地方,用绳子拉船靠岸,开始时,绳长米,且米,拉动绳子将船从点沿方向行驶到点后,绳长米. (1)、试判定的形状,并说明理由;(2)、求船体移动距离的长度.(3)、若在BD段拉动船的速度为1米/秒,到达D后增加了人力,拉动船的速度变为2米/秒,求把船从B拉到岸边A点所用时间.22. 如图,直线经过点 ,
(1)、试判定的形状,并说明理由;(2)、求船体移动距离的长度.(3)、若在BD段拉动船的速度为1米/秒,到达D后增加了人力,拉动船的速度变为2米/秒,求把船从B拉到岸边A点所用时间.22. 如图,直线经过点 , (1)、求直线的表达式;(2)、在直角坐标系中画出的图象,并求出该图象与直线及轴围成图形的面积;(3)、根据图象,直接写出关于的不等式的解集.23. 今年第6号台风“烟花”登录我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,经测量,距离台风中心260km及以内的地区会受到影响.
(1)、求直线的表达式;(2)、在直角坐标系中画出的图象,并求出该图象与直线及轴围成图形的面积;(3)、根据图象,直接写出关于的不等式的解集.23. 今年第6号台风“烟花”登录我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,经测量,距离台风中心260km及以内的地区会受到影响.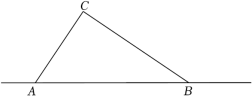 (1)、求∠ACB的度数;(2)、海港C受台风影响吗?为什么?(3)、若台风中心的移动速度为28千米/时,则台风影响该海港持续的时间有多长?24. 对任意一个四位正整数m,如果m的百位数字等于个位数字与十位数字之和,m的千位数字等于十位数字的2倍与个位数字之和,那么称这个数m为“和谐数”.例如: , 满足 , 所以5321是“和谐数”.例如: , 满足 , 但所以8523不是“和谐数”.(1)、判断5413和9588是不是“和谐数”,并说明理由;(2)、若m是“和谐数”,且m与23的和能被11整除,求满足条件的所有“和谐数”m.25. 如图,在平行四边形ABCD中,点G是线段AB上一点,连接CG、DG,满足CG=CD.
(1)、求∠ACB的度数;(2)、海港C受台风影响吗?为什么?(3)、若台风中心的移动速度为28千米/时,则台风影响该海港持续的时间有多长?24. 对任意一个四位正整数m,如果m的百位数字等于个位数字与十位数字之和,m的千位数字等于十位数字的2倍与个位数字之和,那么称这个数m为“和谐数”.例如: , 满足 , 所以5321是“和谐数”.例如: , 满足 , 但所以8523不是“和谐数”.(1)、判断5413和9588是不是“和谐数”,并说明理由;(2)、若m是“和谐数”,且m与23的和能被11整除,求满足条件的所有“和谐数”m.25. 如图,在平行四边形ABCD中,点G是线段AB上一点,连接CG、DG,满足CG=CD. (1)、如图1,过点G作GH⊥CD于点H,若AB=8,GH=2 , 求DG;(2)、如图2,若∠DAB=60°,∠DAB的角平分线交CD于点E,过点E作EF∥AD,满足EF+AG=AD,连接DF、CF,求证:∠DCF=∠GCF.(3)、拓展:如图,正方形ABCD的边长为4 , E为BC上一点,且BE= , F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,直接写出CG的最小值.
(1)、如图1,过点G作GH⊥CD于点H,若AB=8,GH=2 , 求DG;(2)、如图2,若∠DAB=60°,∠DAB的角平分线交CD于点E,过点E作EF∥AD,满足EF+AG=AD,连接DF、CF,求证:∠DCF=∠GCF.(3)、拓展:如图,正方形ABCD的边长为4 , E为BC上一点,且BE= , F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,直接写出CG的最小值.