湖南省张家界市永定区2021-2022学年八年级下学期期末数学试卷
试卷更新日期:2022-07-19 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点A(2,-3)所在的象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 若一个多边形的每个内角都等于150°,则这个多边形的边数是( )A、10 B、11 C、12 D、133. 已知 , , 分别是的三边,根据下列条件能判定为直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 小明3分钟共投篮80次,进了50个球,则小明进球的频率是( )
A、80 B、50 C、1.6 D、0.6255. 已知A(x1 , y1)、B(x2 , y2),是一次函数y=﹣2x+3的图象上的点.当x1>x2时,y1、y2的大小关系为( )A、y1<y2 B、y1>y2 C、y1=y2 D、以上结论都有可能6. 下列各曲线表示的y与x的关系中,y不是x的函数的是( )A、 B、
B、 C、
C、 D、
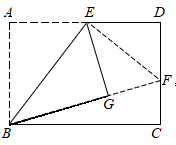
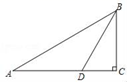
D、 7. 如图,在长方形纸片中, , . 把长方形纸片沿直线折叠,点B落在点E处,交于点F,则的长为( )
7. 如图,在长方形纸片中, , . 把长方形纸片沿直线折叠,点B落在点E处,交于点F,则的长为( ) A、 B、 C、 D、8. 如图,在平面直角坐标系中,对 进行循环往复的轴对称变换,若原来点A坐标是 ,则经过第2021次变换后点A的对应点的坐标为( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,对 进行循环往复的轴对称变换,若原来点A坐标是 ,则经过第2021次变换后点A的对应点的坐标为( )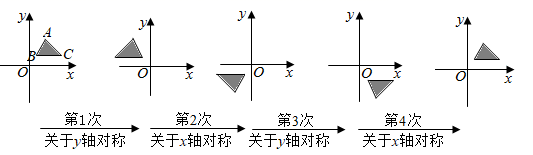 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图所示,小明从坡角为30°的斜坡的山底(A)到山顶(B)共走了200米,则山坡的高度BC为米.
 10. 东东家有一块等腰三角形的空地ABC,如图,已知E,F分别是边AB,AC的中点,量得AB=AC=12米,BC=10米,他想把四边形BCFE用篱笆围成一圈养鸡,则需篱笆长米.
10. 东东家有一块等腰三角形的空地ABC,如图,已知E,F分别是边AB,AC的中点,量得AB=AC=12米,BC=10米,他想把四边形BCFE用篱笆围成一圈养鸡,则需篱笆长米. 11. 已知一组数据有40个,把它分成六组,第一组到第四组的频数分别是5,10,6,7,第五组的频率是0.2,故第六组的频数是 .12. 若点P(m+1,2m)在第四象限,则m的取值范围是.13. 夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥.若荷塘周长为300m,且桥宽忽略不计,则小桥总长为m.
11. 已知一组数据有40个,把它分成六组,第一组到第四组的频数分别是5,10,6,7,第五组的频率是0.2,故第六组的频数是 .12. 若点P(m+1,2m)在第四象限,则m的取值范围是.13. 夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥.若荷塘周长为300m,且桥宽忽略不计,则小桥总长为m.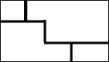 14. 如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(12,5),∠CAO的平分线与y轴相交于点D,则点D的坐标为 .
14. 如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(12,5),∠CAO的平分线与y轴相交于点D,则点D的坐标为 .
三、解答题
-
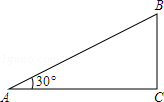
15. 已知y与x-1成正比例,当x=4时,y=27,求:(1)、y与x的函数解析式;(2)、当y=12时,求x的值.16. 如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5cm,求AB的长.
 17. 如图,在矩形ABCD中,点E在边BC上,点F在BC的延长线上,且.求证:四边形AEFD是平行四边形.
17. 如图,在矩形ABCD中,点E在边BC上,点F在BC的延长线上,且.求证:四边形AEFD是平行四边形. 18. 已知:菱形ABCD的两条对角线AC与BD相交于点O,且AC=6,BD=8,求菱形的周长和面积.
18. 已知:菱形ABCD的两条对角线AC与BD相交于点O,且AC=6,BD=8,求菱形的周长和面积.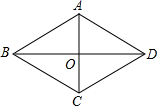 19. 为创建“国家园林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图.
19. 为创建“国家园林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图.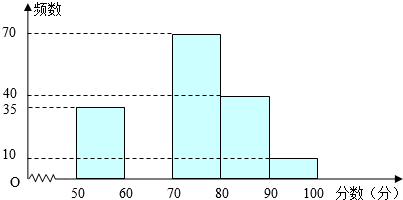
根据以上信息,解答下列问题:
(1)、请补全频数分布直方图;(2)、若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?(3)、比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?20. 如图,、相交于点O, , . (1)、求证:;(2)、若∠ABC=31°,求的度数.21. 明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千静止的时候,踏板离地高一尺(尺),将它往前推进两步(尺),此时踏板升高离地五尺(尺),求秋千绳索(或)的长度.
(1)、求证:;(2)、若∠ABC=31°,求的度数.21. 明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千静止的时候,踏板离地高一尺(尺),将它往前推进两步(尺),此时踏板升高离地五尺(尺),求秋千绳索(或)的长度.