湖北省武汉市武昌区2021-2022学年八年级下学期期末数学试卷
试卷更新日期:2022-07-19 类型:期末考试
一、单选题
-
1. 二次根式在实数范围内有意义,则满足的条件是( )A、 B、 C、 D、2. 下列二次根式是最简二次根式的是( )A、 B、 C、 D、3. 一次函数y=3x+5的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 某校要从四名选手中选取一名同学代表学校参加武汉市“小小外交家”比赛,四名同学平均成绩及其方差如表所示,如果要选择一名成绩好且发挥稳定的选手参赛,则应选择的学生是( )
甲
乙
丙
丁
8
9
9
8
1.2
1.3
1
1
A、甲 B、乙 C、丙 D、丁5. 下列计算正确的是( )A、 B、 C、 D、6. 平面直角坐标系中,点到坐标原点的距离是( )A、2 B、4 C、 D、7. 在四边形中,对角线和交于点 , 下列条件不能判断四边形是平行四边形的是( )A、 , B、 , C、 , D、 ,8. 5名同学周末体育户外运动时间的统计结果如下表,以下说法正确的是( )户外运动时间(小时)
3
3.5
4
4.5
人数
1
1
2
1
A、中位数是2,平均数是3.75 B、中位数是4,平均数是3.75 C、众数是4,平均数是3.8 D、众数是2,平均数是3.89. 在平面直角坐标系中,一次函数的图象可能是( )A、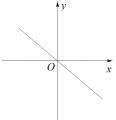 B、
B、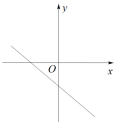 C、
C、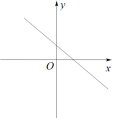 D、
D、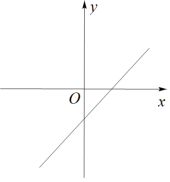 10. 如图,中, , 于点 , , 为斜边的中点,则( )
10. 如图,中, , 于点 , , 为斜边的中点,则( )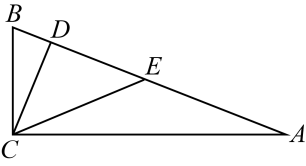 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算:= .
12. 一次函数的图象与轴的交点坐标为;13. 正比例函数的图象与一次函数y=-x+1的图象交于点 , 点的横坐标为2,则这个正比例函数的解析式是.14. 某市在一次空气污染指数抽查中,收集到10天指数数据如下:61,75,81,56,81,91,92,91,75,81.则该组数据的中位数是.15. 小明按照书上的指导,在《几何画板》中绘制了函数的图象,通过观察此函数图象,小明推理出了如下结论:①当时,随的增大而增大;
②当时,有最大值0;
③函数与任意正比例函数一定有交点;
④时,函数的最大值与最小值的差为20.上述结论正确的有.
 16. 如图,在平行四边形中,点在边上,将沿着翻折得到 , 已知 , , , 设 , 当点落在内部(含边上)时,的取值范围.
16. 如图,在平行四边形中,点在边上,将沿着翻折得到 , 已知 , , , 设 , 当点落在内部(含边上)时,的取值范围.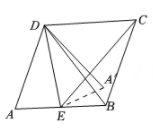
三、解答题
-
17. 计算:(1)、;(2)、.18. 如图,直线与直线交于点.
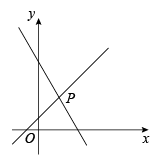 (1)、求 , 的值;(2)、方程组的解为;(3)、根据图象可得不等式的解集为.19. 某灯泡厂测量一批灯泡的使用寿命,从中随机抽查了50只灯泡,它们的使用寿命统计结果如下:
(1)、求 , 的值;(2)、方程组的解为;(3)、根据图象可得不等式的解集为.19. 某灯泡厂测量一批灯泡的使用寿命,从中随机抽查了50只灯泡,它们的使用寿命统计结果如下:调查结果频数统计表
组别
使用寿命
组中值
频数
A
800
5
B
10
C
1600
D
2000
17
E
2400
6

根据以上图表信息,完成下列问题:
(1)、 , ;(2)、这批灯泡的平均使用寿命是多少?(3)、若灯泡使用寿命大于等于1800h则为“超长照明灯泡”,则这批总数为3万只的灯泡里面有多少灯泡属于“超出照明灯泡”?20. 如图,矩形的对角线 , 相交于点 , 且 , . (1)、求证:四边形是菱形;(2)、若 , , 则菱形的面积为.21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,的三个顶点都是格点,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)、求证:四边形是菱形;(2)、若 , , 则菱形的面积为.21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,的三个顶点都是格点,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示. (1)、在图中画出平行四边形 , 为格点;(2)、在边上画一点 , 使得;(3)、找到格点 , 画出直线 , 使得平分平行四边形的面积.22. 某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)、在图中画出平行四边形 , 为格点;(2)、在边上画一点 , 使得;(3)、找到格点 , 画出直线 , 使得平分平行四边形的面积.22. 某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)、求y关于x的函数关系式;(2)、该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)、实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,且限定商店最多购进A型电脑60台,若商店保持同种电脑的售价不变,请你根据以上信息,设计出使这100台电脑销售总利润最大的进货方案.
23. 正方形的边长为4. (1)、如图1,点在上,连接 , 作于点 , 于点.
(1)、如图1,点在上,连接 , 作于点 , 于点.①求证:;
②如图2,对角线 , 交于点 , 连接 , 若 , 求的长;
(2)、如图3,点在的延长线上, , 点在的延长线上, , 点在上,连接 , 在的右侧作 , , 连接.点从点沿方向运动,当点运动到中点时,设的中点为 , 当点运动到点时,设的中点为 , 直接写出的长为.24. 如图,在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 点是轴正半轴上一点,且. (1)、直接写出点的坐标为 , 直线的解析式为;(2)、设点在直线上,点在轴上,连接 , 以为边向右侧作正方形.
(1)、直接写出点的坐标为 , 直线的解析式为;(2)、设点在直线上,点在轴上,连接 , 以为边向右侧作正方形.①在点的运动过程中,当顶点落在直线上时,求点的坐标;
②点从点运动到点的过程中,正方形的对角线交点运动的路径长为 ▲ .