(人教版)2022-2023学年度第一学期八年级数学第13章 轴对称 单元测试
试卷更新日期:2022-07-18 类型:单元试卷
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,在△ABC中,DE是AC的垂直平分线,分别交BC,AC于D,E两点,若∠B=80°,∠C=35°,则∠BAD的度数为( )
2. 如图,在△ABC中,DE是AC的垂直平分线,分别交BC,AC于D,E两点,若∠B=80°,∠C=35°,则∠BAD的度数为( ) A、65° B、35° C、30° D、25°3. 如图,在中,是的垂直平分线,的周长为 , 的周长为 , 则的长为( )
A、65° B、35° C、30° D、25°3. 如图,在中,是的垂直平分线,的周长为 , 的周长为 , 则的长为( ) A、 B、 C、 D、4. 点关于x轴的对称点坐标为( )A、 B、 C、 D、5. 如图所示,在平面直角坐标系xOy中,△ABC关于直线y=1对称,已知点A的坐标是(3,4),则点B的坐标是( )
A、 B、 C、 D、4. 点关于x轴的对称点坐标为( )A、 B、 C、 D、5. 如图所示,在平面直角坐标系xOy中,△ABC关于直线y=1对称,已知点A的坐标是(3,4),则点B的坐标是( )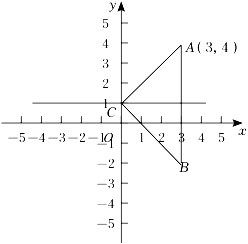 A、(3,﹣4) B、(﹣3,2) C、(3,﹣2) D、(﹣2,4)6. 如图,△ABC中, , D是BC的中点, , 则∠BAD的度数为( )
A、(3,﹣4) B、(﹣3,2) C、(3,﹣2) D、(﹣2,4)6. 如图,△ABC中, , D是BC的中点, , 则∠BAD的度数为( ) A、25° B、50° C、65° D、100°7. 如图,在中,运用尺规作图的方法在BC边上取一点P,使 , 下列作法正确的是( )A、
A、25° B、50° C、65° D、100°7. 如图,在中,运用尺规作图的方法在BC边上取一点P,使 , 下列作法正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,是等边三角形,D是BC边上一点,于点E.若 , 则DC的长为( )
8. 如图,是等边三角形,D是BC边上一点,于点E.若 , 则DC的长为( ) A、4 B、5 C、6 D、79. 如图,已知是平分线上的一点, , , 是的中点, , 如果是上一个动点,则的最小值为( )
A、4 B、5 C、6 D、79. 如图,已知是平分线上的一点, , , 是的中点, , 如果是上一个动点,则的最小值为( )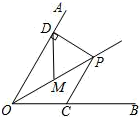 A、 B、 C、 D、10. 如图, ,点 为 内一点,点 分别在 上,当 的周长最小时, 的度数是( )
A、 B、 C、 D、10. 如图, ,点 为 内一点,点 分别在 上,当 的周长最小时, 的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
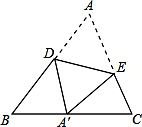
11. 如图,△ABC中,∠A=60°将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′DB=50°,那么∠A′ED的度数为 .
 12. 如图,△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M、N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为.
12. 如图,△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M、N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为. 13. 若点与点关于x轴对称,则m+n= .14. 如图, 是一角度为 的锐角木架,要使木架更加牢固,需在其内部添加一些连接支撑木件 、 、 …,且 …,在 、 足够长的情况下,如果最多能添加这样的连接支撑木件为6根,则锐角 的范围为.
13. 若点与点关于x轴对称,则m+n= .14. 如图, 是一角度为 的锐角木架,要使木架更加牢固,需在其内部添加一些连接支撑木件 、 、 …,且 …,在 、 足够长的情况下,如果最多能添加这样的连接支撑木件为6根,则锐角 的范围为. 15. 如图,在△ABC中,AB=AC,BC=5,△ABC的面积为20,DE垂直平分AC,分别交边AB,AC于点D,E,点F为直线DE上一动点,点G为BC的中点,连接FG,FC,则FC+FG的最小值为 .
15. 如图,在△ABC中,AB=AC,BC=5,△ABC的面积为20,DE垂直平分AC,分别交边AB,AC于点D,E,点F为直线DE上一动点,点G为BC的中点,连接FG,FC,则FC+FG的最小值为 .
三、解答题
-
16. 如图,在直角 中, , 的平分线 交 于点 ,若 垂直平分 ,求 的度数.
 17. 如图,在 中, ,DE垂直平分AC.若 ,求 的度数.
17. 如图,在 中, ,DE垂直平分AC.若 ,求 的度数.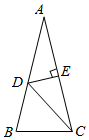 18. 如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
18. 如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
①画出△ABC关于x轴的对称图形△A1B1C1;
②将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2 , 写出顶点A2 , B2 , C2的坐标.
19. 如果△ABC关于x轴进行轴对称变换后,得到△A1B1C1 , 而△A1B1C1关于y轴进行轴对称变换后,得到△A2B2C2 , 若△ABC三个顶点坐标分别为A(-2,3)、B(-4,2)、C(-1,0),请你分别写出△A1B1C1与△A2B2C2各顶点坐标.




