（人教版）2022-2023学年度第一学期八年级数学13.3.1 等腰三角形 同步测试
试卷更新日期：2022-07-18 类型：同步测试
一、单选题
-
1. 若等腰三角形的一个外角是70°，则它的底角的度数是（ ）A、110° B、70° C、35° D、55°2. 如图， ，在 上取点C，以点C为圆心， 长为半径画弧交 于点D，连接 ；以点D为圆心， 长为半径画弧交 于点E，连接 ， 的度数为（ ）
A、20° B、25° C、30° D、35°3. 如图，B在AC上，D在CE上， ， ， 的度数为（ ）
A、50° B、65° C、75° D、80°4. 等腰三角形的一个内角是 ，则它底角的度数是（ ）A、 B、 或 C、 或 D、5. 已知 的周长是16，且 ，又 ，D为垂足，若 的周长是12，则AD的长为（ ）A、7 B、6 C、5 D、46. 如图，在△ABC中，AB=BC，AD⊥BC于点D，CE平分∠ACB交AB于点E，交AD于点P，若∠B=x°，则∠APE的度数为（ ）
A、 B、 C、 D、7. 如图，△ABC≌△EDC，BC⊥CD，点A，D，E在同一条直线上，∠ACB＝25°，则∠ADC的度数是（ ）
A、45° B、60° C、75° D、70°8. 如图，是等腰三角形， ， ， BP平分；点D是射线BP上一点，如果点D满足是等腰三角形，那么的度数是（ ）.
A、20°或70° B、20°、70°或100° C、40°或100° D、40°、70°或100°9. 如图，线段AB，BC的垂直平分线 ， 相交于点O.若 ， 则（ ）
A、50° B、80° C、90° D、100°10. 如图，在 中， 是BC边上的高，点 在AD上，且 ，则△ABC的面积为s，则是△ABE的面积是（ ）
A、 B、 C、 D、二、填空题
-
11. 等腰三角形的一边长是2cm，另一边长是4cm，则底边长为cm.12. 如图，在 ABC中，AB＝AC，∠A＝36°，点D在AC上，且BD＝BC，则∠BDC＝.
13. 如图， 、 的平分线相交于点F，过F作 ，交 于点D，交 于点E， ， ，则 .
14. 如图， 平分 交 于点E，若 ，则 .
15. 如图， ，点P在 的边 上，以点P为圆心， 为半径画弧，交 于点A，连接 ，则 .
三、解答题
-
16.如图， △ABC中， AB=AC ，D、E分别是AB、AC上的点，且 ∠ABE=∠ACD ，BE、CD交于点O，求证： △OBC是等腰三角形.
17. 如图，在△ABC中，AB＝AC，高BD、CE相于点O.证明OB＝OC.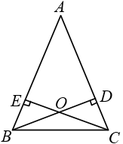
18. 如图，在等腰△ABC中，BA=BC，AD平分∠BAC，DE∥AC，求证：∠ADB=3∠EDA．
19. 已知：如图，AD是等腰三角形ABC的底边BC上的中线，DE∥AB，交AC于点E．求证：△AED是等腰三角形．
20. 如图，在△ABC中，AB＝AC，∠A＝36°，AB的垂直平分线交AB于点D，交AC于点E．求证：△BEC是等腰三角形．
21. 等腰三角形一腰上的中线把这个三角形的周长分成12cm和21cm两部分，求这个等腰三角形的底边长.22. 如图，△ABC中，AB=AC=CD，BD=AD，求△ABC中∠CAB的度数
23. 如图，已知∠AOB，作∠AOB的平分线OC，将直角尺DEMN如图所示摆放，使EM边与OB边重合，顶点D落在OA边上，DN边与OC交于点P． 猜想△DOP是三角形什么三角形？；并说明理由
24. “三等分角”是被称为几何三大难题的三个古希腊作图难题之一．如图1所示的“三等分角仪”是利用阿基米德原理做出的．这个仪器由两根有槽的棒PA，PB组成，两根棒在P点相连并可绕点P旋转，C点是棒PA上的一个固定点，点A，O可在棒PA，PB内的槽中滑动，且始终保持OA＝OC＝PC．∠AOB为要三等分的任意角．则利用“三等分角仪”可以得到∠APB ＝∠AOB．我们把“三等分角仪”抽象成如图2所示的图形，完成下面的证明．
已知：如图2，点O，C分别在∠APB的边PB，PA上，且OA＝OC＝PC．
求证：∠APB ＝∠AOB．
