（人教版）2022-2023学年度第一学期八年级数学13.2.2 用坐标表示轴对称同步测试

试卷更新日期：2022-07-18 类型：同步测试

进入出卷网下载

一、单选题

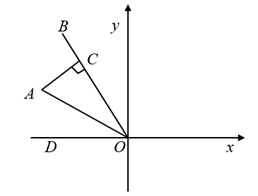
1. 在平面直角坐标系中，点B的坐标是 $(4 ， - 1)$ ，点A与点B关于y轴对称，则点A的坐标是（）

A、 $(4 ， 1)$ B、 $(- 1 ， 4)$ C、 $(- 4 ， - 1)$ D、 $(- 1 ， - 4)$

查看试题解析
2. 在平面直角坐标系中，点 $(2 ， - 1)$ 关于x轴的对称点的坐标是（）

A、 $(- 2 ， 1)$ B、 $(2 ， 1)$ C、 $(- 2 ， - 1)$ D、 $(- 1 ， 2)$

查看试题解析
3. 已知图形A全部在x轴的上方，如果将图形A上的所有点的纵坐标都乘以－1，横坐标不变得到图形B，则（）

A、两个图形关于x轴对称 B、两个图形关于y轴对称 C、两个图形重合 D、两个图形不关于任何一条直线对称

查看试题解析
4. 若平面直角坐标系中的两点A（a，3），B（1，b）关于y轴对称，则a＋b的值是（）

A、2 B、-2 C、4 D、-4

查看试题解析
5. 若一个点A的横坐标不变，纵坐标乘以﹣1后得到一个点B，则（　　）

A、点A与点B关于x轴对称 B、点A与点B关于y轴对称 C、点A与点B关于原点对称 D、点A向x轴的负方向平移1个单位得点B

查看试题解析
6. 如图，OA平分∠BOD，AC⊥OB于点C，且AC=2，已知点A到y轴的距离是3，那么点A关于x轴对称的点的坐标为（　　）

A、(2，3) B、(3，2) C、(-2，-3) D、(-3，-2)

查看试题解析
7. 在平面直角坐标系中，点 $A$ 的坐标是 $(- 2 ， 1)$ ，点 $B$ 与点 $A$ 关于 $y$ 轴对称，则点 $B$ 的坐标是（）

A、 $(1 ， - 2)$ B、 $(2 ， - 1)$ C、 $(2 ， 1)$ D、 $(- 1 ， - 2)$

查看试题解析
8. 在平面直角坐标系中，已知点A（﹣2，a）和点B（b，﹣3）关于y轴对称，则ab的值（）

A、﹣1 B、1 C、6 D、﹣6

查看试题解析
9. 若点 $A (x ， 1)$ 与 $B (- 2 ， y)$ 关于 $x$ 轴对称，则（）．

A、 $x = - 2$ ， $y = 1$ B、 $x = - 2$ ， $y = - 1$ C、 $x = 2$ ， $y = - 1$ D、 $x = 2$ ， $y = 1$

查看试题解析
10. 已知点P（3，2x﹣4）关于x轴的对称点在第一象限，则x的取值范围是（）

A、x＞2 B、x＜2 C、x＞0 D、x＜0

查看试题解析

二、填空题

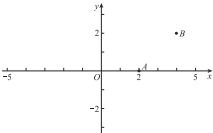
11. 若点P(-1，3)与点P'(a+1，3)关于y轴对称，则a为.

查看试题解析
12. 如图，在平面直角坐标系xOy中，点A（2，0），B（4，2），若点P在x轴下方，且以O，A，P为顶点的三角形与 $△$ OAB全等，则满足条件的P点的坐标是．

查看试题解析
13. 若点 $M (a ， 3)$ ， $N (- 4 ， b)$ 关于x轴对称，则b的值为．

查看试题解析
14. 点P（3，2）关于y轴的对称点的坐标是．

查看试题解析
15. 若点 $A (a - 2 ， 3)$ 和点 $B (- 1 ， b + 5)$ 关于y轴对称，则点 $C (a ， b)$ 在第象限．

查看试题解析

三、解答题

16. 已知点A（a+2b，﹣1），B（﹣2，a﹣b），若点A、B关于y轴对称，求a+b的值.

查看试题解析
17. 已知点 $A (2 a - b ， 5 + a)$ ， $B (2 b - 1 ， - a + b)$ .若 $A$ 、 $B$ 关于 $y$ 轴对称，求 ${(4 a + b)}^{2020}$ 的值．

查看试题解析
18. 已知点 $A (- 1, 3 a - 1)$ 与点 $B (2 b + 1, - 2)$ 关于 $y$ 轴对称，求点 $A 、 B$ 的坐标.

查看试题解析
19. 如图，△ABC中，已知点A(-1，4)，B(-2，2)，C(1，1).

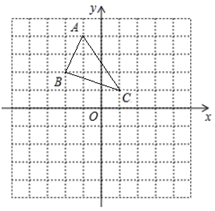(1)、作ΔABC关于x轴对称的△A₁B₁C₁ ，并写出点A₁ ， B₁ ， C₁的坐标，

(2)、作△ABC关于y轴对称的△A₂B₂C₂ ，并写出点A₂ ， B₂ ， C₂的坐标，

(3)、观察点A₁ ， B₁ ， C₁和A₂ ， B₂ ， C₂的坐标，请用文字语言归纳点A₁和A₂ ， B₁和B₂ ， C₁和C₂坐标之间的关系.

查看试题解析
20. 如图，是由4×4个大小完在一样的小正方形组成的方格纸，其中有两个小正方形是涂黑的，请再选择三个小正方形并涂黑，使图中涂黑的部分成为轴对称图形.并画出它的一条对称轴(如图例.画对一个得1分)

查看试题解析
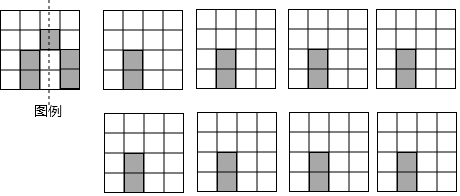21. 如图，图中的小方格都是边长为1的正方形，
①直接写出△ABC的各顶点坐标：
A（，），B （，），C （，）；
②画出△ABC关于y轴的对称图形△A₁B₁C₁；
③直接写出△ABC关于x轴对称的△A₂B₂C₂的顶点A₂ （，） B₂ （，） (其中A₂与A对应，B₂与B对应，不必画图．)

查看试题解析
22. 如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（-3，2），B（0，4），C（0，2）．画出△ABC关于x轴对称的△A₁B₁C₁并写出点A₁的坐标；A₁（，）．

查看试题解析
23. 如图，在平面直角坐标系中，A(-1，5)，B(-1，0)，C(-4，3)．

(1)、求出△ABC的面积；

(2)、在图中作出△ABC关于y轴的对称图形△A₁B₁C₁；

(3)、写出点A₁ ， B₁ ， C₁的坐标．

查看试题解析
24. 已知某个图形是按下面方法连接而成的：（0，0）→（2，0）；（1，0）→（0，﹣1）；（1，1）→（1，﹣2）；（1，0）→（2，﹣1）．

(1)、请连接图案，它是一个什么汉字？

(2)、作出这个图案关于y轴的轴对称图形，并写出新图案相应各端点的坐标，你得到一个什么汉字？

查看试题解析

（人教版）2022-2023学年度第一学期八年级数学13.2.2 用坐标表示轴对称 同步测试

一、单选题

二、填空题

三、解答题

（人教版）2022-2023学年度第一学期八年级数学13.2.2 用坐标表示轴对称同步测试