(人教版)2022-2023学年度第一学期八年级数学13.1.2 线段的垂直平分线的性质 同步测试
试卷更新日期:2022-07-18 类型:同步测试
一、单选题
-
1. 如图,在△ABC中,BC的垂直平分线交AB于点D,交BC于点E,若∠A=50°,∠DCB=2∠ACD,则∠B的度数为( )
 A、26° B、36° C、52° D、45°2. 如图,在△ABC中,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于M、N两点,连接MN,交AB于点H,以点H为圆心,HA的长为半径作的弧恰好经过点C,以点B为圆心,BC的长为半径作弧交AB于点D,连接CD,若∠A=22°,则∠BDC=( )
A、26° B、36° C、52° D、45°2. 如图,在△ABC中,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于M、N两点,连接MN,交AB于点H,以点H为圆心,HA的长为半径作的弧恰好经过点C,以点B为圆心,BC的长为半径作弧交AB于点D,连接CD,若∠A=22°,则∠BDC=( ) A、52° B、55° C、56° D、60°3. 如图,在△ABC中,分别以点A和点C为圆心,大于AC的长为半径画弧交于两点,过这两点作直线交AC于点E,交BC于点D,连接AD.若△ADB的周长为15,AE=4,则△ABC的周长为( )
A、52° B、55° C、56° D、60°3. 如图,在△ABC中,分别以点A和点C为圆心,大于AC的长为半径画弧交于两点,过这两点作直线交AC于点E,交BC于点D,连接AD.若△ADB的周长为15,AE=4,则△ABC的周长为( ) A、17 B、19 C、21 D、234. 如图,在中, , , 于点D,AB的垂直平分线交AB于点E,交BC于点F,连接AF,则的度数为( ).
A、17 B、19 C、21 D、234. 如图,在中, , , 于点D,AB的垂直平分线交AB于点E,交BC于点F,连接AF,则的度数为( ). A、20° B、30° C、35° D、70°5. 如图,在中, , AC的垂直平分线MN交BC于点N,且 , 则的度数是( )
A、20° B、30° C、35° D、70°5. 如图,在中, , AC的垂直平分线MN交BC于点N,且 , 则的度数是( ) A、45° B、50° C、55° D、60°6. 如图,在△ABC中,AB的垂直平分线EF分别交AB、AC边于点E、F,点K为EF上一动点,则BK+CK的最小值是以下条线段的长度( )
A、45° B、50° C、55° D、60°6. 如图,在△ABC中,AB的垂直平分线EF分别交AB、AC边于点E、F,点K为EF上一动点,则BK+CK的最小值是以下条线段的长度( )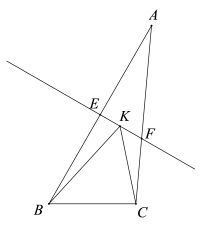 A、EF B、AB C、AC D、BC7. 下列选项中的尺规作图,能推出PA=PC的是( )A、
A、EF B、AB C、AC D、BC7. 下列选项中的尺规作图,能推出PA=PC的是( )A、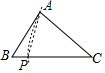 B、
B、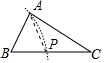 C、
C、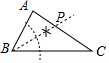 D、
D、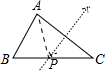 8. 如图是李老师在黑板上演示的尺规作图及其步骤,
8. 如图是李老师在黑板上演示的尺规作图及其步骤,已知钝角 ,尺规作图及步骤如下:
步骤一:以点 为圆心, 为半径画弧;
步骤二:以点 为圆心, 为半径画弧,两弧交于点 ;
步骤三:连接 ,交 延长线于点 .

下面是四位同学对其做出的判断:
小明说: ;
小华说: ;
小强说: ;
小方说: .
则下列说法正确的是( )
A、只有小明说得对 B、小华和小强说的都对 C、小强和小方说的都不对 D、小明和小方说的都对9. 如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( ). A、在 AC、BC 两边高线的交点处 B、在 AC、BC 两边垂直平分线的交点处 C、在 AC、BC 两边中线的交点处 D、在∠A、∠B两内角平分线的交点处10. 到三角形三个顶点距离相等的点是( )A、三边高线的交点 B、三条中线的交点 C、三边垂直平分线的交点 D、三条内角平分线的交点
A、在 AC、BC 两边高线的交点处 B、在 AC、BC 两边垂直平分线的交点处 C、在 AC、BC 两边中线的交点处 D、在∠A、∠B两内角平分线的交点处10. 到三角形三个顶点距离相等的点是( )A、三边高线的交点 B、三条中线的交点 C、三边垂直平分线的交点 D、三条内角平分线的交点二、填空题
-
11. 如图,已知的周长为13,根据图中尺规作图的痕迹,若 , 则的周长为.
 12. 已知:如图,在中, , 线段AB的垂直平分线分别交AB、AC于点D、E,如果 , 那么 .
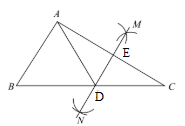
12. 已知:如图,在中, , 线段AB的垂直平分线分别交AB、AC于点D、E,如果 , 那么 . 13. 如图,在中, , 以点A为圆心,AB长为半径作弧交BC于点D,交AC于点E.再分别以点C,D为圆心,大于的长为半径作弧,两弧相交于F,G两点.作直线FG.若直线FG经过点E,则的度数为°.
13. 如图,在中, , 以点A为圆心,AB长为半径作弧交BC于点D,交AC于点E.再分别以点C,D为圆心,大于的长为半径作弧,两弧相交于F,G两点.作直线FG.若直线FG经过点E,则的度数为°. 14. 如图,∠ , 是 , 垂直平分线的交点,则的度数是 .
14. 如图,∠ , 是 , 垂直平分线的交点,则的度数是 . 15. 如图,已知 中, , , ,作AC的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第一条线段 ;作 的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第二条线段 ;作 的垂直平分线交AB于点 、交 于点 ,连接 ,得到第三条线段 ;……,如此作下去,则第n条线段 的长为 .
15. 如图,已知 中, , , ,作AC的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第一条线段 ;作 的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第二条线段 ;作 的垂直平分线交AB于点 、交 于点 ,连接 ,得到第三条线段 ;……,如此作下去,则第n条线段 的长为 .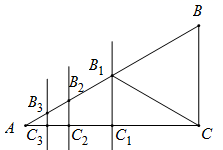
三、解答题
-
16. 如图,在 中, , 平分 交 于点D, 于点E,且E为 的中点.求 的度数.
 17. 如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,求AC的长.
17. 如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,求AC的长. 18. 如图,在 中, 是 的中垂线,分别交 , 于点D,E.若 的周长为8, ,求 的长.
18. 如图,在 中, 是 的中垂线,分别交 , 于点D,E.若 的周长为8, ,求 的长. 19. 已知:如图,在△ABC中,∠ABC的平分线BP与AC边的垂直平分线PQ交于点P,过点P分别作PD⊥AB于点D,PE⊥BC于点E,若BE=10cm,AB=6cm,求CE的长.
19. 已知:如图,在△ABC中,∠ABC的平分线BP与AC边的垂直平分线PQ交于点P,过点P分别作PD⊥AB于点D,PE⊥BC于点E,若BE=10cm,AB=6cm,求CE的长. 20. 如图,在 中, 是 的垂直平分线.已知 的周长为 求 的周长.
20. 如图,在 中, 是 的垂直平分线.已知 的周长为 求 的周长.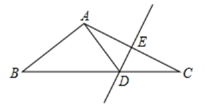 21. 如图,在△ABE中,AD⊥BE于点D,C是BE上一点,BD=DC,且点C在AE的垂直平分线上,若△ABC的周长为18 cm,求DE的长.
21. 如图,在△ABE中,AD⊥BE于点D,C是BE上一点,BD=DC,且点C在AE的垂直平分线上,若△ABC的周长为18 cm,求DE的长.