山西省临汾市侯马市2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-07-18 类型：期末考试

进入出卷网下载

一、单选题

1. 某班级计划在耕读园里搭三角形围栏，可以选择三种长度的木条组合是（）

A、3、4、8 B、4、4、8 C、3、5、6 D、5、6、11

查看试题解析
2. 2022年2月4日中国将举办第24届冬季奥林匹克运动会，这是中国历史上第一次举办冬季奥运会，下面是本届冬奥会及往届冬奥会的会徽，其中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如果不等式（a﹣4）x＞a-4的解集为x＜1，则a应满足（）

A、a＜4 B、a＞﹣4 C、a＞4 D、a＜﹣4

查看试题解析
4. 你知道吗？现在世界上最古老的方程出现在英国考古学家莱茵德1858年找到的一份古埃及人的“纸草书”上．在我国，“方程”一词最早出现于东汉初年的一部数学著作中，这部著作的名称是（）

A、《周髀算经》 B、《九章算术》 C、《五经算术》 D、《孙子算经》

查看试题解析
5. 如图为一张锐角三角形纸片ABC，小明想要通过折纸的方式折出如下线段：①BC边上的中线AD，②BC边上的角平分线AE，③BC边上的高AF．根据所学知识与相关活动经验可知：上述三条线中，所有能够通过折纸折出的有（）

A、①② B、①③ C、②③ D、①②③

查看试题解析
6. 为了更有效地展开体育锻炼，某班将参加体育锻炼的同学进行分组，如果每组8人，则多余4人；如果每组10人，则还缺6人，若参加体育锻炼的有x人，则下列所列方程中正确的是（）

A、 $8 x + 4 = 10 x - 6$ B、 $8 x - 4 = 10 x + 6$ C、 $\frac{x - 4}{8} = \frac{x + 6}{10}$ D、 $\frac{x + 4}{8} = \frac{x - 6}{10}$

查看试题解析
7. 如图所示，在长为50米，宽为40米的长方形地块上，有纵横交错的几条小路（图中阴影部分），宽均为1米，其他部分均种植花草，则道路的面积是（）

A、50平方米 B、40平方米 C、90平方米 D、89平方米

查看试题解析
8. 如图，将直角三角形ABC绕着它的直角顶点C顺时针旋转90°得到△A´B´C，连接AA´，若 $∠ 1 = 25 °$ ，则∠BAA´的度数是（）

A、65 $°$ B、60 $°$ C、55 $°$ D、50 $°$

查看试题解析
9. 用正三角形和正六边形镶嵌，若每一个顶点周围有m个正三角形、n 个正六边形，则m，n满足的关系式是( )

A、2m+3n=12 B、m+n=8 C、2m+n=6 D、m+2n=6

查看试题解析
10. 6月18日，最开始是京东的周年庆，2013年后，618就成了各大电商平台的网购节了．在618当日，小梦在某电商平台上选择了甲乙丙三种商品，当购物车内选3件甲，2件乙，1件丙时显示价格为420元；当选2件甲，3件乙，4件丙时显示价格为580元，那么购买甲、乙、丙各两件时应该付款（）

A、200元 B、400元 C、500元 D、600元

查看试题解析

二、填空题

11. 世界最长跨海大桥——港珠澳大桥，主桥为三座大跨度钢结构斜拉桥，斜拉式大桥采用三角形结构，使其不易变形，这种做法的依据是.

查看试题解析
12. 如图为《北京2022年冬残奥会会徽》纪念邮票，其规格为边长14.92毫米的正八边形，则正八边形的内角和为.

查看试题解析
13. 将直角三角形ABC沿CB方向平移BE的距离后，得到直角三角形DEF，已知AG＝4，BE＝7，DE＝10，则阴影部分的面积．

查看试题解析
14. 已知一个等腰三角形的两边长a，b满足方程组 ${\begin{matrix} 2 a - b = 3, \\ a + b = 3, \end{matrix}$ 则此等腰三角形的周长为.

查看试题解析
15. 若一个三角形中一个角的度数是另一个角的度数的3倍，则称这样的三角形为“和谐三角形”.例如，三个内角分别为 $120 °$ ， $40 °$ ， $20 °$ 的三角形是“和谐三角形”，如图，直角三角形 $A B C$ 中， $∠ C A B = 90 °$ ， $∠ A B C = 60 °$ ， $D$ 是边 $C B$ 上一动点.当 $△ A D C$ 是“和谐三角形”时， $∠ D A B$ 的度数是.

查看试题解析

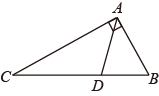
三、解答题

16. 解方程或方程组

(1)、 $3 (2 x - 1) - (x - 1) = 2 (8 - 2 x)$

(2)、 ${\begin{array}{l} 2 x + y = 2 \\ 8 x + 3 y = 9 \end{array}$

查看试题解析
17. 阅读下面解不等式 $\frac{x - 1}{3} - \frac{x + 2}{6}$ > $\frac{x - 4}{2}$ 的过程，完成任务：
解： $2 x - 2 - x + 2 > 3 x - 12$ …第一步
$2 x - x - 3 x > - 12$ ……第二步
$- 2 x > - 12$ … 第三步
$x > 6$ …… 第四步

(1)、任务一：第一步去分母的依据是；

(2)、第步开始出现不符合题意，这一步错误的原因是；直接写出正确结果是．

(3)、任务二：请你根据平时的学习经验，就解不等式时需要注意的事项给其他同学提出建议．

查看试题解析
18. 如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点， $△$ ABC的顶点均在格点上，O、M也在格点上．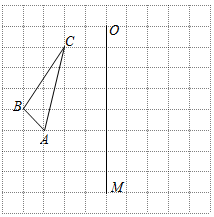
（ 1 ）作出 $△$ ABC关于直线OM对称的 $△$ A₁B₁C₁；
（ 2 ）作出 $△$ ABC绕点A按顺时针方向旋转90°后所得的 $△$ AB₂C₂；
（ 3 ）在OM上做出点P，使 $△$ PBC的周长最小．

查看试题解析
19. 如图，六边形ABCDEF的内角都相等．

(1)、若∠1＝60°，求∠ADC的度数；

(2)、AB与ED有怎样的位置关系？为什么？

查看试题解析
20. 已知关于x、y的方程满足方程组 ${\begin{array}{l} 3 x + 2 y = m + 1 \\ 2 x + y = m - 1 \end{array}$ ．

(1)、若 $x - y = 2$ ，求m的值；

(2)、若x、y均为非负数，求m的取值范围，并化简式子 $| m - 3 | + | m - 5 |$ ；

查看试题解析
21. 核酸检测是直接找到病毒存在的证据，它作为诊断新冠肺炎的一个标准，具有重要意义，开展全员核酸检测既有利于精准防控，保护群众健康，又有助于人员的合理流动，推动社会经济和生活秩序的全面恢复.2022年6月，山西省某市从疫情防控大局出发，降低核酸检测价格，提高核酸检测普及率，价格调整情况如表：
项目
1∶1单样检测
10∶1混样检测
调价前（元/次/人）
28
8
调价后（元/次/人）
16
4

(1)、某公司开展员工核酸检测，第一次核酸检测时（调价前），共抽取100人进行检测，选择的是1∶1单样检测和10∶1混样检测两种方式，共花费1640元，求1∶1单样检测和10∶1混检测的各有多少人？

(2)、为节省费用，第二次进行全员核酸检测时（调价后），全公司共计1100人进行检测，拟安排一部分人员进行1∶1单样检测，其余人员进行10∶1混样检测，且所花总费用不超过5600元，那么最多可安排1：1单样检测的多少人？

查看试题解析
22. 如图①，△ABC和△ADE中，∠BAC=∠DAE=90°，∠ABC=∠ADE=45°，点D、E分别在边AB、AC上

(1)、如图②，将△ADE绕点A逆时针旋转到如图位置，若∠BAD=30°，求∠BAE的度数；

(2)、如图②，在（1）的基础上继续旋转，当旋转角度α=时，直线AC与DE垂直；（0°＜α≤360°）

(3)、如图③，△ADE绕点A在平面内自由旋转，连接BD，且AD=4，AB=10，求BD的最大值和最小值．

查看试题解析
23. 如图①，∠MON＝90°，点A，B分别在OM，ON上运动（不与点O重合）．

(1)、若BC是∠ABN的平分线，BC的反向延长线与∠BAO的平分线交于点D．
①若∠BAO＝60°，则∠D＝ ▲ °；
②猜想：∠D的度数是否随A，B的运动而发生变化？并说明理由；

(2)、若∠ABC＝ $\frac{1}{3}$ ∠ABN，∠BAD＝ $\frac{1}{3}$ ∠BAO，求∠D的度数；

查看试题解析

项目	1∶1单样检测	10∶1混样检测
调价前（元/次/人）	28	8
调价后（元/次/人）	16	4