山东省淄博市周村区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-07-18 类型:期末考试
一、单选题
-
1. 下列命题中,真命题是( )A、两个锐角的和一定大于直角 B、内错角相等 C、不带根号的数一定是有理数 D、两点之间线段最短2. 已知 是二元一次方程 的一组解,则a的值为( )A、2 B、 C、1 D、3. 如图,直线 , 等腰直角的两个顶点、分别落在直线、上,AC⊥BC,垂足为点C,若∠1=16°,则∠2的度数是( )
 A、34° B、29° C、24° D、19°4. 在数轴上表示不等式的解集,正确的是( )A、
A、34° B、29° C、24° D、19°4. 在数轴上表示不等式的解集,正确的是( )A、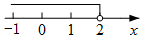 B、
B、 C、
C、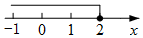 D、
D、 5. 若m>n ,则下列不等式中一定成立的是( )A、m+2<n+3 B、2m<3n C、-m<-n D、ma2>na26. 等腰三角形的一个角是 , 则它的底角是( )A、 B、 C、或 D、或7. 如图,Rt△ABC中,B=90,点P在边AB上,CP平分∠ACB,PB=3cm,AC=10cm,则△APC的面积是( )
5. 若m>n ,则下列不等式中一定成立的是( )A、m+2<n+3 B、2m<3n C、-m<-n D、ma2>na26. 等腰三角形的一个角是 , 则它的底角是( )A、 B、 C、或 D、或7. 如图,Rt△ABC中,B=90,点P在边AB上,CP平分∠ACB,PB=3cm,AC=10cm,则△APC的面积是( ) A、15cm2 B、22.5cm2 C、30cm2 D、45cm28. 若m为任意实数,点(2m+1,m-2)一定不在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,△ABC≌△DEC,点E在线段AB上,∠B=75°,则∠ACD的度数为( )
A、15cm2 B、22.5cm2 C、30cm2 D、45cm28. 若m为任意实数,点(2m+1,m-2)一定不在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,△ABC≌△DEC,点E在线段AB上,∠B=75°,则∠ACD的度数为( ) A、30° B、25° C、20° D、15°10. 如图,在△ABC中,∠BAC=80°,边AB的垂直平分线交AB于点D,交BC于点E,边AC的垂直平分线交AC于点F,交BC于点G,连接AE,AG.则∠EAG的度数为( )
A、30° B、25° C、20° D、15°10. 如图,在△ABC中,∠BAC=80°,边AB的垂直平分线交AB于点D,交BC于点E,边AC的垂直平分线交AC于点F,交BC于点G,连接AE,AG.则∠EAG的度数为( ) A、35° B、30° C、25° D、20°11. 如图所示,已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边OB上,PM=PN,若MN=2,则OM的长为( )
A、35° B、30° C、25° D、20°11. 如图所示,已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边OB上,PM=PN,若MN=2,则OM的长为( ) A、3 B、4 C、5 D、612. 如图所示的正方形网格中,网格线的交点称为格点.已知A,B是两个格点,如果点C也是图形中的格点,且△ABC为等腰三角形,所有符合条件的点C有( )
A、3 B、4 C、5 D、612. 如图所示的正方形网格中,网格线的交点称为格点.已知A,B是两个格点,如果点C也是图形中的格点,且△ABC为等腰三角形,所有符合条件的点C有( ) A、3个 B、4个 C、5个 D、6个
A、3个 B、4个 C、5个 D、6个二、填空题
-
13. 已知关于x,y的方程组 , 则 .14. 如果不等式(a﹣3)x>a﹣3的解集是x<1,那么a的取值范围是 .15. 在一个不透明的袋子中装有3个红球和若干个白球,每个球除颜色外都相同,任意摸出一个球,摸出红球的概率是 , 则白球的个数是 .16. 在实数范围内定义一种新运算“⊕”,其运算规则为:a⊕b=2a+3b.如:1⊕5=2×1+3×5=17.则不等式x⊕4<0的解集为 .17. 如图,在△ABC中,AB=AC,点D,E,F分别是BC,AC,AB上的点,且BF=CD,BD=CE,∠FDE=α,则∠A的度数是度(用含α的代数式表示).

三、解答题
-
18. 解下列方程组:(1)、(2)、19. 解不等式(组):(1)、(2)、20. 如图,在△ABC中,点D是BC上一点,且AD=AB, , ∠BAD=∠CAE,连接DE交AC于点F.
 (1)、若∠B=70°,求∠C的度数:(2)、若AE=AC.求证:AD平分∠BDE.21. 阅读下列材料:
(1)、若∠B=70°,求∠C的度数:(2)、若AE=AC.求证:AD平分∠BDE.21. 阅读下列材料:小明在一本数学杂志上看到一道有意思的数学题:解不等式 , 根据绝对值的几何意义,到原点距离小于1的点在数轴上集中在-1和+1之间,如图:

所以,该不等式的解集为 .
因此,不等式的解集为或 .
根据以上方法小明继续探究了不等式的解集,即到原点的距离大于2小于5的点的集合就集中在这样的区域内,如图:

所以,不等式的解集为-5<x<-2或2<x<5.
仿照小明的做法解决下面问题:
(1)、不等式的解集为;(2)、不等式的解集是;(3)、不等式的解集是 .22. 为更好地推进生活垃圾分类工作,改善城市生态环境,某小区准备购买A,B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元,购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.(1)、每个A型垃圾箱和B型垃圾箱分别是多少元?(2)、若该小区物业计划用低于2150元的资金购买A,B两种型号的垃圾箱共20个,且至少购买6个B型垃圾箱,请问有几种购买方案?

