山东省烟台市龙口市2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-07-18 类型：期末考试

进入出卷网下载

一、单选题

1. 若a＜b，则下列各式中一定成立的是（）

A、a+2＞b+2 B、a-2＞b-2 C、-2a＞-2b D、 $\frac{a}{2}$ ＞ $\frac{b}{2}$

查看试题解析
2. 下列事件中，是不可能事件的是（）

A、明天会下雨 B、早上的太阳从东方升起 C、射击运动员射击一次，命中9环 D、度量三角形的内角和，结果是90°

查看试题解析
3. 分别写有数字－1，－2，1，3，4的五张卡片，除数字外其他均相同，将它们背面朝上，从中任抽一张，抽到负数的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{1}{3}$ C、 $\frac{2}{5}$ D、 $\frac{1}{2}$

查看试题解析
4. 下列命题是假命题的是（）

A、等角的余角相等 B、两直线平行，内错角相等 C、同旁内角互补，两直线平行 D、三角形的外角大于任何一个内角

查看试题解析
5. 如图，在△ABC中，∠ABC=90°，AD平分∠BAC交BC于D，BC=14cm，点D到AC的距离为5cm，则CD的长为（）

A、7cm B、8cm C、9cm D、10cm

查看试题解析
6. 一副三角板如图所示放置，两三角板的斜边互相平行，每个三角板的直角顶点都在另一个三角板的斜边上，图中∠α的度数为（）

A、75° B、60° C、45° D、30°

查看试题解析
7. 如图，△ABC中，∠BAC=90^o ， AC=6cm，AB=8cm，作边AB的垂直平分线DE交BC于点D，△ADC的周长为（）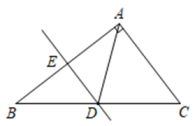

A、12cm B、14cm C、16cm D、18cm

查看试题解析
8. 某射击运动员在同一条件下的射击成绩记录如下：
射击次数
20
40
100
200
400
1000
“射中9环以上”的次数
15
33
78
158
321
801
“射中9环以上”的频率
0.75
0.825
0.78
0.79
0.8025
0.801
则该运动员“射中9环以上”的概率约为（结果保留一位小数）（）

A、0.7 B、0.75 C、0.8 D、0.9

查看试题解析
9. 我国古代数学名著《孙子算经》中记载：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何?”意思是：用一根绳子去量一根木条，绳子还剩余4.5尺；将绳子对折再量木条，木条剩余1尺，问木条长多少尺?如果设木条长x尺，绳子长y尺，那么可列方程组为（）

A、 ${\begin{cases} y = x + 4.5 \\ 0.5 y = x - 1 \end{cases}$ B、 ${\begin{cases} y = x + 4.5 \\ y = 2 x - 1 \end{cases}$ C、 ${\begin{cases} y = x - 4.5 \\ 0.5 y = x + 1 \end{cases}$ D、 ${\begin{cases} y = x - 4.5 \\ y = 2 x - 1 \end{cases}$

查看试题解析
10. 若不等式2x+5＜1的解集中x的每一个值都能使关于x的不等式4x+1＜x-m成立，则m的取值范围是（）

A、m＞5 B、m≤5 C、m≥5 D、m＜-5

查看试题解析

二、填空题

11. 把“同角的余角相等”改成“如果……，那么……”：．

查看试题解析
12. 小明在求二元一次方程x+2y=10的一个正整数解时，他已求出了y的值为3，则x的值应为.

查看试题解析
13. 如图，在正方形网格中，点A，B，C，D均在格点上，则∠ABC+∠BCD＝°．

查看试题解析
14. 为确保信息安全，信息需加密传输，发送方将明文加密为密文传输给接收方，接收方收到密文后解密还原为明文.若某种加密规则为：明文m、n对应的密文为m-3n，2m+3n．例如：明文1，2对应的密文是-5，8．当接收方收到密文是6，3，则解密后得到的明文是．

查看试题解析
15. 如图，如果小球在用七巧板拼成的正方形中自由地滚动，并随机地停留在某区域，它最终停留在2号区域的概率为．

查看试题解析
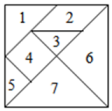16. 如图，∠C＝90°，AC＝20，BC＝10，AX⊥AC，点P和点Q同时从点A出发，分别在线段AC和射线AX上运动，且AB＝PQ，当AP＝时，以点A，P，Q为顶点的三角形与△ABC全等．

查看试题解析

三、解答题

17. 解方程组：

(1)、 ${\begin{array}{l} x = 2 y \\ x - y = 6 \end{array}$

(2)、 ${\begin{array}{l} x - y = 2 \\ 4 x + y = 3 \end{array}$

查看试题解析
18. 解不等式组 ${\begin{array}{l} \frac{x}{2} > \frac{x - 1}{3} \\ 3 (x + 1) \geq 4 x + 2 \end{array}$ ，并在数轴上表示出其解集．

查看试题解析
19. 如图1和图2均是一个均匀的可以自由转动的转盘，图1被平均分成9等份，分别标有1，2，3，4，5，6，7，8，9这9个数字．转动转盘，当转盘停止后，指针指向的数字即为转出的数字（当指针恰好指在分界线上时重转）；图2被涂上红色与绿色，转动转盘，当转盘停止后，指针指向的颜色即为转出的颜色（当指针恰好指在分界线上时重转）．小明转动图1的转盘，小亮转动图2的转盘．

(1)、求小明转出的数字是偶数的概率．

(2)、小颖认为，小明转出来的数字小于7的概率与小亮转出的颜色是红色的概率相同，她的看法对吗？为什么？

查看试题解析
20. 如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交CE的延长线于F，且AF=BD．求证：AD是△ABC的中线．

查看试题解析
21. 如图，已知∠1=50°，∠2=130°，DA平分∠BDF，∠3=∠4，求∠CBD的度数．

查看试题解析
22. 在平面直角坐标系中，直线y=- $\frac{3}{4}$ x+ $\frac{3}{4}$ 与y= $\frac{3}{2}$ x+3交于点A，

(1)、求点A的坐标；

(2)、根据图象直接写出不等式- $\frac{3}{4}$ x+ $\frac{3}{4}$ ＞ $\frac{3}{2}$ x+3的解集

查看试题解析
23. 一个不透明的袋中装有红、黄、白三种颜色的球共10个，它们除了颜色外完全相同，其中黄球个数比白球个数的3倍少2个，从袋中摸出一个球是黄球的概率为0.4.

(1)、求袋中红、黄、白三种颜色的球的个数；

(2)、向袋中放入若干个红球，使摸出一个球是红球的概率为0.7，求放入红球的个数；

(3)、在（2）的条件下，求摸出一个球是白球的概率.

查看试题解析
24. 尺规作图（不写作法，保留作图痕迹）
已知：线段a，h（如图）.
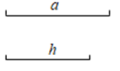
求作：△ABC，使AB=AC，且BC=a，高AD=h.

查看试题解析
25. 为了增强市民的环保意识，我市准备印制一批宣传册.该宣传册每本共10张彩页，由A、B两种彩页构成．已知A种彩页印刷费3元/张，B种彩页印刷费2元/张，一本宣传册印刷费共计24元．

(1)、每本宣传册A、B两种彩页各有多少张？（列方程组解答）

(2)、据了解，印刷的数量超过1 000本时，印刷费用打八折．若使印刷费不超过3.2万元，预计最多能印刷多少本？

查看试题解析
26. 数学理解

(1)、如图1，在等边 $△ A B C$ 内，作 $D B = D C$ ，且 $∠ B D C = 80 °$ ， E是 $△ D B C$ 内一点，且 $∠ C B E = 10 °$ ， $B E = B D$ ，求 $∠ B C E$ 的度数；

(2)、如图2，在 $△ D B C$ 中， $D B = D C$ ， $∠ B D C = 80 °$ ， E是 $△ D B C$ 内一点，且 $∠ C B E = 10 °$ ， $∠ B C E = 30 °$ ，连接DE，求 $∠ C D E$ 的度数．

查看试题解析

射击次数	20	40	100	200	400	1000
“射中9环以上”的次数	15	33	78	158	321	801
“射中9环以上”的频率	0.75	0.825	0.78	0.79	0.8025	0.801