山东省潍坊市潍城区等六区2021-2022学年七年级下学期期末考试数学试题

试卷更新日期：2022-07-18 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，点A的坐标是（）．

A、 $(- 2 ， 4)$ B、（2，4） C、（4，2） D、 $(- 4 ， 2)$

查看试题解析
2. 如图，已知A为直线l外一定点，B为直线l上一动点．则下列说法正确的是（）．

A、当点B自左向右移动时，A，B两点间的距离越来越小 B、连接AB，则线段AB的长度即为点A到直线l的距离 C、过点A有且只有一条直线与直线l平行 D、同一平面内，过点A有两条直线与直线l垂直

查看试题解析
3. 在计算器上输入一个绝对值小于1的非零小数，再按 $=$ 键，这个数会被化为科学记数法的形式 $2 \times 1 0^{- 23}$ ，则这个数是（）．

A、 $\underset{22 个 0}{\underset{︸}{0.00 \cdot \cdot \cdot 0}} 2$ B、 $\underset{23 个 0}{\underset{︸}{0.00 \cdot \cdot \cdot 0}} 2$ C、 $\underset{24 个 0}{\underset{︸}{0.00 \cdot \cdot \cdot 0}} 2$ D、 $\underset{25 个 0}{\underset{︸}{0.00 \cdot \cdot \cdot 0}} 2$

查看试题解析
4. 在数学实践课上，小亮经研究发现：在如图所示的 $△ A B C$ 中，连接点A和BC上的一点D，线段AD等分 $△ A B C$ 的面积，则AD是 $△ A B C$ 的（）．

A、高线 B、中线 C、角平分线 D、对角线

查看试题解析
5. 如图，圆环中大圆的半径为r，小圆的半径为长 $\frac{r}{2}$ ， AB为大圆的直径，则阴影部分的面积为（）．

A、 $\frac{π r^{2}}{4}$ B、 $\frac{3 π r^{2}}{4}$ C、 $\frac{π r^{2}}{8}$ D、 $\frac{3 π r^{2}}{8}$

查看试题解析
6. 若单项式 $20 x^{m - n} y^{14}$ 与 $\frac{2}{5} x^{3} y^{3 m - 8 n}$ 可以合并成一项，则 $m^{n}$ 的值是（）．

A、 $\frac{1}{2}$ B、2 C、 $- \frac{1}{2}$ D、 $- 2$

查看试题解析
7. 《孙子算经》记载：今有3人共车，二车空；二人共车，九人步，问人与车各几何？译文：今有若干人乘车，若每三人乘一辆车，最终剩余2辆车；若每2人乘一辆车，最终剩余9人无车可乘．问共有多少人？多少辆车？如果设有x人，y辆车，则可列方程组为（）．

A、 ${\begin{array}{l} x + 6 = 3 y ， \\ 2 y + 9 = x \end{array}$ B、 ${\begin{array}{l} x - 3 y = 6 ， \\ 2 y - x = 9 \end{array}$ C、 ${\begin{array}{l} x + 3 y = 6 ， \\ 2 y + x = 9 \end{array}$ D、 ${\begin{array}{l} x - 6 = 3 y ， \\ x - 2 y = 9 \end{array}$

查看试题解析
8. 已知 $x^{2} - x = 3$ ，则代数式 $(3 x + 2) (3 x - 2) + x (x - 10)$ 的值为（）．

A、34 B、14 C、26 D、7

查看试题解析

二、多选题

9. 下列各式计算错误的是（）．

A、 ${(- a^{3} b)}^{2} = - a^{6} b^{2}$ B、 $4 a^{2} \cdot 3 a = 12 a^{3}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 $2 a (a - 1) = 2 a^{2} - 2$

查看试题解析
10. 已知等腰三角形的周长是12，且各边长都为整数，则各边的长可能是（）．

A、2，2，8 B、5，5，2 C、4，4，4 D、3，3，5

查看试题解析
11. 如图， $A B ∥ C D$ ， EF交AB，CD于点M，N，连接DA并延长交EF于点E，连接BC并延长交EF于点F．下列结论正确的是（）．

A、 $∠ 1 = ∠ 2$ B、 $∠ 3 = ∠ B$ C、 $∠ E = ∠ F$ D、 $∠ 4 = ∠ 5$

查看试题解析
12. 若 $x^{2} - 2 (k - 1) x + 4$ 是完全平方式，则k的值为（）．

A、 $- 2$ B、 $- 1$ C、2 D、3

查看试题解析

三、填空题

13. $46 ° 2 4^{'} =$ $°$ ．

查看试题解析
14. 六边形的外角和五边形的外角和（在横线上填“＞”，“＜”或“＝”）．

查看试题解析
15. 学校位于小亮家北偏西60°方向，距离为500米，那么小亮家相对于学校的位置可以描述为．

查看试题解析
16. 如图，可以用量角器量出 $∠ A O B$ 的度数，则 $∠ A O B$ 的补角是 $°$ ．

查看试题解析
17. 已知 $W = m a + m b + m c$ ，当 $a = 19.7$ ， $b = 32.5$ ， $c = 35.8$ ， $m = 2.5$ 时， $W =$ ．

查看试题解析
18. 若 $a^{n} = b$ （ $a > 0$ 且 $a \neq 1$ ， $b > 0$ ），则n叫做以a为底b的对数，记为 $l o g_{a} b$ （即 $l o g_{a} b = n$ ），如 $2^{5} = 32$ ，则5叫做以2为底32的对数，记 $l o g_{2} 32$ （即 $l o g_{2} 32 = 5$ ）．根据以上运算规则可得 $l o g_{3} 81 =$ ．

查看试题解析

四、解答题

19.

(1)、计算与化简：① $2^{- 2} + {(\frac{11}{7} - π)}^{0} - {(- \frac{1}{2})}^{3}$ ；
② ${(x - y)}^{2} \cdot {(x - y)}^{4} \div {(y - x)}^{5}$ ；

(2)、因式分解：① $m^{2} - 2 m n + n^{2}$ ；② ${(1 + m)}^{2} - {(2 - m)}^{2}$ ；

(3)、先化简，再求值： $a (a - 2 b) - {(a + 1)}^{2} + 2 a$ ，其中 $a = - \frac{1}{4}$ ， $b = 2$ ．

查看试题解析
20. 解方程组：

(1)、 ${\begin{array}{l} 2 x + 3 y = 4 ， \\ x + 2 y = 3 ； \end{array}$

(2)、 ${\begin{array}{l} \frac{x}{2} + \frac{y}{5} = \frac{4}{5} ， \\ 3 (x - 2) = 4 (y + 1) . \end{array}$

查看试题解析
21. 小莹和小亮是学校运动会彩旗方阵的队员，如图，方格纸中每个小正方形的边长都是1个单位长度，小莹和小亮分别在点 $A (3 ， 2)$ ， $B (- 1 ， 2)$ 的位置．请完成下列问题：

(1)、请在方格纸中画出适当的以O为坐标原点的直角坐标系；

(2)、彩旗方队是以AB为边的正方形，请在图中画出正方形ABCD，并写出点C，D的坐标；

(3)、求出以A，B，O三点为顶点的三角形的面积．

查看试题解析
22. 如图，BE，DF分别平分 $∠ D B C$ ， $∠ A D B$ ，且BE∥DF．请说明： $∠ C + ∠ A D C = 180 °$ ．

查看试题解析
23. 小莹和小亮每人带了16元钱到学校附近的文具店购买中性笔和笔记本，他们要购买的中性笔每盒10支，如果整盒买比单支买每支可优惠0.2元．小莹要买2支中性笔和3本笔记本共需花费14元；小亮要买8支中性笔和2本笔记本共需花费16元．

(1)、单独购买一支中性笔多少元？每本笔记本的单价是多少元？

(2)、小莹和小亮都还想再买一件单价为1.5元的小工艺品，他们利用所带的钱，能否做到既买全了想要的文具，又都能买到一件小工艺品？请通过运算说明．

查看试题解析
24. 在四边形ABCD中， $∠ A = 80 °$ ， $∠ D = 140 °$ ．

(1)、如图①，若 $∠ B = ∠ C$ ，求出 $∠ B$ 的度数；

(2)、如图②，若 $∠ D C B$ 的角平分线交AB于点E，且 $E C ∥ A D$ ，求出 $∠ B$ 的度数；

(3)、如图③，若 $∠ A B C$ 和 $∠ D C B$ 的角平分线交于点E，求出 $∠ B E C$ 的度数．

查看试题解析
25. 如图①，现有边长分别为a，b的正方形硬纸板A和B，邻边长为a和b（ $a > b$ ）的长方形硬纸板C若干．

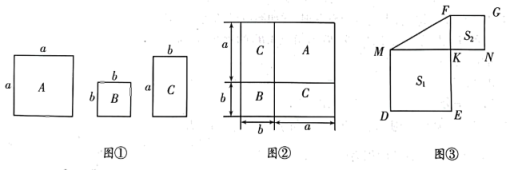(1)、活动课上，老师用图①中的1张正方形A，1张正方形B和2张长方形C纸板，排成了如图②中的大正方形．观察图形，由图②可以得到的等式为（等号两边用含a，b的代数式表示）；

(2)、小莹想用图①的三种纸板拼一个面积为 $(a + b) (a + 2 b)$ 的大长方形，则需要A硬纸板张，B硬纸板张，C硬纸板张（空格处填写数字），并参考图②画出该大长方形的设计图（画出一种即可）；

(3)、如图③，已知点K为线段MN上的动点，分别以MK，NK为边在MN的两侧作正方形MKED和正方形NKFG，面积分别记作 $S_{1}$ ， $S_{2}$ ，若 $M N = 8$ ， △MKF的面积为6，利用（1）中得到的结论求 $S_{1} + S_{2}$ 的值．

查看试题解析