广东省梅州市大埔县2021-2022学年七年级下学期期末考试数学试题
试卷更新日期:2022-07-18 类型:期末考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、等腰三角形 B、正方形 C、圆 D、平行四边形2. 将0.0000012用科学记数法表示应为( )A、 B、 C、 D、3. 用下列长度的三根木棒首尾相接,能做成三角形框架的是( )A、1,2,3 B、2,3,4 C、2,7,4 D、2,5,74. 下列运算正确的是( )A、 B、 C、 D、5. 下列计算中,能用平方差公式的是( )A、 B、 C、 D、6. 一个小球在如图所示的地板上自由滚动,并随机停在某块方砖上.如果每一块方砖除颜色外完全相同,那么小球最终停留在黑砖上的概率是( )
 A、 B、 C、 D、7. 如图,下列选项中,不能判定a//b的是( )
A、 B、 C、 D、7. 如图,下列选项中,不能判定a//b的是( )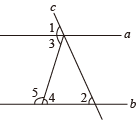 A、 B、 C、 D、8. 已知b∥c,将一块含角的直角三角尺按如图的方式放置(等于),其中 , 两点分别落在直线 , 上,若 , 则为( )
A、 B、 C、 D、8. 已知b∥c,将一块含角的直角三角尺按如图的方式放置(等于),其中 , 两点分别落在直线 , 上,若 , 则为( )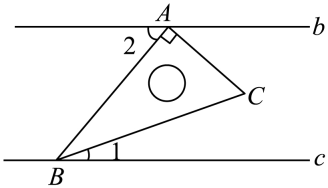 A、 B、 C、 D、9. 小华同学喜欢锻炼,周六他先从家跑步到新华公园,在那里与同学打一会羽毛球后又步行回家,下面能反映小华离家距离 与所用时间 之间关系的图象是( )A、
A、 B、 C、 D、9. 小华同学喜欢锻炼,周六他先从家跑步到新华公园,在那里与同学打一会羽毛球后又步行回家,下面能反映小华离家距离 与所用时间 之间关系的图象是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,在△ABC中,BD平分∠ABC,E是BC的中点, 过点E作BC的垂线交BD于点F,连结CF。若∠A=50°,∠ACF=40°,则∠CFD的度数为( )
10. 如图,在△ABC中,BD平分∠ABC,E是BC的中点, 过点E作BC的垂线交BD于点F,连结CF。若∠A=50°,∠ACF=40°,则∠CFD的度数为( ) A、30° B、45° C、55° D、60°
A、30° B、45° C、55° D、60°二、填空题
-
11. 计算: .12. 如图,直线a,b被直线c所截,且 , , 则的度数为
 13. 在如图所示的转盘中,转出的可能性最大的颜色是 .
13. 在如图所示的转盘中,转出的可能性最大的颜色是 . 14. 若a﹣b=1,ab=﹣2,则(a﹣2)(b+2)=.15. 自变量x与因变量y的关系式为: , 当x每增加1时,y增加 .16.
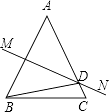
14. 若a﹣b=1,ab=﹣2,则(a﹣2)(b+2)=.15. 自变量x与因变量y的关系式为: , 当x每增加1时,y增加 .16.如图,△ABC中AB=AC,AB的垂直平分线MN交AC于点D.若AC+BC=10cm,则△DBC的周长为 .
 17. 如图,四边形均为正方形,其中正方形面积为 . 图中阴影部分面积为 , 正方形面积为 .
17. 如图,四边形均为正方形,其中正方形面积为 . 图中阴影部分面积为 , 正方形面积为 .
三、解答题
-
18. 计算下列各式:(1)、;(2)、;19. 先化简,再求值:(a-2b)(a+2b)-(a-2b)2+8b,其中a=-6,b= .20. 在一个不透明的袋子中装有除颜色外都相同的黄球、绿球和红球共12个,其中红球有2个.(1)、摸到红球的概率是;(2)、若摸到绿球的概率是 ,求袋子中黄球的个数.21. 在所给网格图(每小格均为边长是1的正方形)中,的位置如图所示,点A,B,C都在格点上.
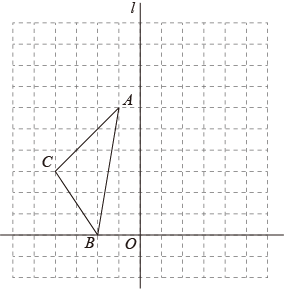 (1)、请在图中画出关于直线l对称的图形;(2)、计算出的面积.22. 如图,已知 , 点D在线段上,求证:// .
(1)、请在图中画出关于直线l对称的图形;(2)、计算出的面积.22. 如图,已知 , 点D在线段上,求证:// . 23. 小明家、新华书店、学校在一条笔直的公路旁,某天小明骑车上学,当他骑了一段后,想起要买某本书,于是又返回到刚经过的新华书店,买到书后继续骑车去学校,他本次骑车上学的过程中离家距离与所用的时间的关系如图所示,请根据图象提供的信息回答下列问题:
23. 小明家、新华书店、学校在一条笔直的公路旁,某天小明骑车上学,当他骑了一段后,想起要买某本书,于是又返回到刚经过的新华书店,买到书后继续骑车去学校,他本次骑车上学的过程中离家距离与所用的时间的关系如图所示,请根据图象提供的信息回答下列问题: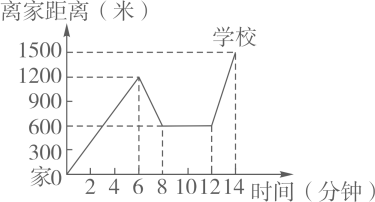 (1)、小明家到学校的距离是米;小明在书店停留了分钟;(2)、如果骑车的速度超过了300米/分就超越了安全限度,小明买到书后继续骑车到学校的这段时间的骑车速度在安全限度内吗?请说明理由;(3)、请直接写出小明出发后多长时间离家的距离为900米?24.(1)、如图1,与中, , B、C、E三点在同一直线上, , 则 .
(1)、小明家到学校的距离是米;小明在书店停留了分钟;(2)、如果骑车的速度超过了300米/分就超越了安全限度,小明买到书后继续骑车到学校的这段时间的骑车速度在安全限度内吗?请说明理由;(3)、请直接写出小明出发后多长时间离家的距离为900米?24.(1)、如图1,与中, , B、C、E三点在同一直线上, , 则 . (2)、如图2,在中, , 过点C作 , 且 , 求的面积.
(2)、如图2,在中, , 过点C作 , 且 , 求的面积. 25. 问题解决:
25. 问题解决: (1)、问题情境:如图1所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到P的距离之和最短?请画出点P的位置;(2)、问题理解:如图2,在△ABC中,AB=AC,AD平分∠BAC,点E是AC边的中点,点P是线段AD上的动点,画出PC+PE取得最小值时点P的位置;(3)、问题运用:如图3,在△ABC中,AB=AC=13,BC=10,AD=12,AD是∠BAC的平分线,当点E、P分别是AC和AD上的动点时,求PC+PE的最小值.
(1)、问题情境:如图1所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到P的距离之和最短?请画出点P的位置;(2)、问题理解:如图2,在△ABC中,AB=AC,AD平分∠BAC,点E是AC边的中点,点P是线段AD上的动点,画出PC+PE取得最小值时点P的位置;(3)、问题运用:如图3,在△ABC中,AB=AC=13,BC=10,AD=12,AD是∠BAC的平分线,当点E、P分别是AC和AD上的动点时,求PC+PE的最小值.