广东省江门市新会区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-07-18 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数是无理数的是（）

A、0 B、 $\sqrt{4}$ C、3.14 D、 $\sqrt{5}$

查看试题解析
2. $\sqrt{81}$ 的算术平方根是（）

A、3 B、 $\pm 3$ C、 $\pm 9$ D、9

查看试题解析
3. 如图，点O在直线AB上， $O C ⊥ O D$ ，若 $∠ B O D = 32 °$ ，则∠AOC＝（）

A、 $120 °$ B、 $122 °$ C、 $132 °$ D、 $112 °$

查看试题解析
4. 已知二元一次方程组 ${\begin{array}{l} a - 2 b = 4 \\ 2 a - b = 3 \end{array}$ ，则 $a + b =$ （）

A、1 B、－1 C、7 D、－7

查看试题解析
5. 下列表述中，能确定具体位置点的是（）

A、江门市新会区会城启超大道 B、北偏东 $2 0^{∘}$ C、点A在y轴正半轴上 D、东经 $11 8^{∘}$ ，北纬 $5 0^{∘}$

查看试题解析
6. 若 $m = \sqrt{65} - 2$ ，则实数m所在范围是（）

A、 $4 < m < 5$ B、 $5 < m < 6$ C、 $6 < m < 7$ D、 $7 < m < 8$

查看试题解析
7. 在第二象限内的点P（x，y），满足 $| x | = 9$ ， $y^{2} = 4$ ，则点P的坐标是（）

A、（9，2） B、（9，－2） C、（－9，2） D、（－9，－2）

查看试题解析
8. 《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等.交易其一，金轻十三两.问金、银一枚各重几何？”.意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相等.两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计）.问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两，根据题意得（）

A、 ${\begin{array}{l} 11 x = 9 y \\ （ 10 y + x ） - （ 8 x + y ） = 13 \end{array}$ B、 ${\begin{array}{l} 10 y + x = 8 x + y \\ 9 x + 13 = 11 y \end{array}$ C、 ${\begin{array}{l} 9 x = 11 y \\ （ 8 x + y ） - （ 10 y + x ） = 13 \end{array}$ D、 ${\begin{array}{l} 9 x = 11 y \\ （ 10 y + x ） - （ 8 x + y ） = 13 \end{array}$

查看试题解析
9. 一组随机抽样的样本数据最大值是120，最小值是58，画频数分布直方图时，要将这组数据进行分组，若取组距为5，则组数是（）

A、10 B、11 C、12 D、13

查看试题解析
10. 关于x的不等式 $3 x - m + 2 > 0$ 的最小整数解为2，则实数m的取值范围是（）

A、 $5 \leq m < 8$ B、 $5 < m < 8$ C、 $5 \leq m \leq 8$ D、 $5 < m \leq 8$

查看试题解析

二、填空题

11. $| \sqrt{3} - \sqrt{5} | =$ ．

查看试题解析
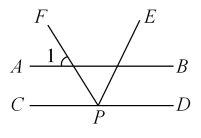
12. 学校为了解本校七年级学生的身体素质，从七年级全体学生共320人中随机抽取了80人进行身体素质测试，这次抽样调查的样本容量是．

查看试题解析
13. 如图， $A B ∥ C D$ ，点P为CD上一点，PF是∠EPC的平分线，若 $∠ 1 = 5 8^{∘}$ ，则∠EPD的大小是．

查看试题解析
14. 已知 $△$ ABC三个顶点的坐标分别是A（0，3）、B（2，－2）、C（－5，1），将 $△$ ABC平移后顶点A的对应点 $A_{1}$ 的坐标是（2，4），则顶点B的对应点 $B_{1}$ 的坐标是．

查看试题解析
15. 一只纸箱重量为0.8kg，放入苹果后，纸箱和苹果的总重量不能超过10kg，若每个苹果的平均重量为0.25kg，则这只纸箱装苹果个数不能超过个．

查看试题解析
16. 在平面直角坐标系中，点P（x，y）满足 ${(5 x - 2 y - 10)}^{2} + | 3 x + 2 y - 6 | = 0$ ，则点P的坐标是．

查看试题解析
17. 已知关于x的不等式组 ${\begin{array}{l} \frac{3 x - 5}{2} > x + a \\ \frac{3 - 2 x}{9} \leq - 3 \end{array}$ 的解集为 $x \geq 15$ ，那么所有满足条件的正整数a的值之和是．

查看试题解析

三、解答题

18. 计算： $\sqrt{48} + \sqrt{{(- 3)}^{2}} - | - \sqrt{3} | - \sqrt[3]{27}$ ．

查看试题解析
19. 解方程组： ${\begin{array}{l} 4 (x - y - 1) + 3 (y - 1) = - 2 \\ \frac{x}{2} + \frac{y}{3} = 2 \end{array}$

查看试题解析
20. 解不等式： $\frac{5 x + 1}{6} - 2 > \frac{x - 5}{4}$ .

查看试题解析
21. 解不等式组 ${\begin{array}{l} 2 (x + 1) > 3 x - 4 \\ \frac{4 x + 1}{3} - \frac{3 x + 1}{2} \leq 1 \end{array}$

查看试题解析
22. 为满足防疫需要，学校要储备抗疫物资，购进甲、乙两款医用口罩共250盒，甲、乙两款医用口罩分别是20元/盒、30元/盒，共花了6500元．

(1)、甲、乙两款医用口罩各购进多少盒？

(2)、已知甲、乙两款医用口罩每盒的口罩数量分别是50个/盒、100个/盒，按照防疫要求，学校必须储备足够使用10天的口罩，学校师生共900人，按每人每天储备2个口罩计算，问购买的口罩数量是否满足防疫要求？

查看试题解析
23. 如图，点O在直线AB上， $C O ⊥ A B$ ， $∠ 2 - ∠ 1 = 34 °$ ， OE是∠AOD的平分线， $O F ⊥ O E$ ．

(1)、求∠AOE的度数．

(2)、求∠BOF的度数．

查看试题解析
24. 学校为了解七年级学生每个学期参加综合实践活动的情况，随机抽取了部分七年级学生进行问卷调查，了解一个学期参加综合实践活动的天数情况，并用得到的数据绘制了下面两幅不完整的统计图作为素材，命制数学试题，请你根据图中提供的信息，回答下列问题：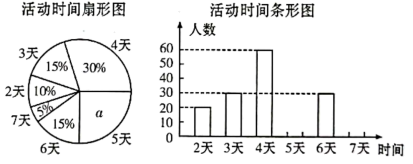

(1)、求出扇形统计图中的a值，并求出该校七年级学生的总人数．

(2)、求出活动时间分别为5天、7天的学生人数，并补全条形统计图．

(3)、求出扇形统计图中“活动时间为4天”所在扇形的圆心角度数．

查看试题解析
25. 如图，已知AB∥CD，若∠C=35∘，AB是∠FAD的平分线.

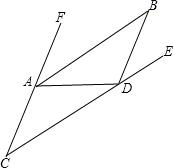(1)、求∠FAD的度数；

(2)、若∠ADB=110∘，求∠BDE的度数.

查看试题解析